Regresní metriky
V úvodním příkladu s krajinou jsme si metriku vymýšleli sami. Existuje samozřejmě řada standardním metrik, které se k hodnocení modelů používají. Uvedeme si přehled nejnámějších z nich:
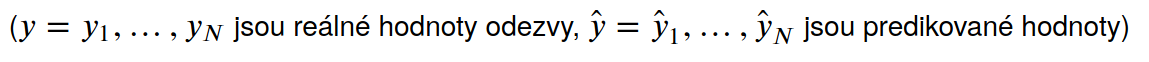
MAE (Mean absolute error) - průměr absolutních hodnot odchylek požadovaných výstupů od predikovaných výstupů
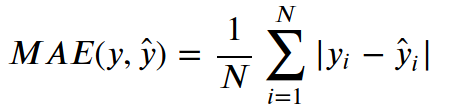
MSE (Mean squared error) - průměr sumy čterců odchylek požadovaných výstupů od predikovaných výstupů
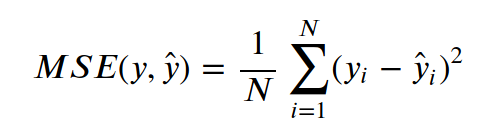
R2 score (Koeficient determinace) - koeficient determinace vyjadřuje, jaký podíl variability závislé proměnné (odezvy) model vyjadřuje. Dá se interpretovat tak, že říká, jak moc je náš model lepší než konstantní baseline daná jako průměr.
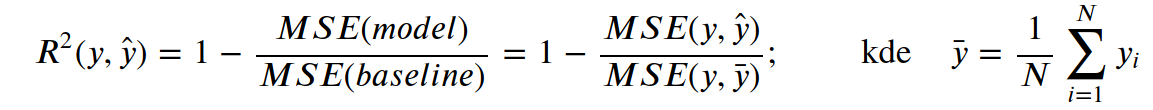
R2 skóre dosahuje maximálně hodnoty jedna, což znamená dokonalou predikci.
Pokud nemáš ráda vzorečky, nelam si s nimi hlavu. Podívej se na následující příklad:
Vytvoříme dataframe, který bude obsahovat odezvy (sloupec "správně") a predikované hodnoty (sloupec "predikováno"). Pro jednoduchost hodnoty odezvy vygenerujeme náhodně a jejich "predikce" vytvoříme tak, že k těmto odezvám přičteme náhodné číslo z intervalu (-10, 10).
import pandas as pd
import random
df = pd.DataFrame({"správně": [random.randint(10, 90) for _ in range(10)]})
df["predikováno"] = df["správně"].apply(lambda predikovano: predikovano + random.randint(-10, 10))
df
Spočteme si MSE, MAE a $R^2$ skóre. Napišme si na to funkci:
def spocti_metriky(skutecna_odezva, predikovano):
chyby = pd.DataFrame()
chyby["absolutní_chyba"] = abs(skutecna_odezva - predikovano)
chyby["chyba_na_druhou"] = (skutecna_odezva - predikovano)**2
baseline = skutecna_odezva.mean()
chyby["chyba_na_druhou_baseline"] = (skutecna_odezva - baseline)**2
MSE = chyby["chyba_na_druhou"].mean()
MAE = chyby["absolutní_chyba"].mean()
R2 = 1 - MSE/chyby["chyba_na_druhou_baseline"].mean()
return chyby, MSE, MAE, R2
df_chyby, MSE, MAE, R2 = spocti_metriky(df["správně"], df["predikováno"])
# zobrazme si tabulku spolu s odpovídajícími chybami
pd.concat([df, df_chyby], axis="columns")
# vypišme si hodnoty metrik
print(f"MSE = {MSE}")
print(f"MAE = {MAE}")
print(f"R2 = {R2}")
Z tabulky výše i ze zobrazených chyb vidíme, že MSE daleko více penalizuje větší chyby.
Zkusme si ještě nasimulovat řešení, které bude poměrně přesné (náhodná odchylka, kterou přičítáme, bude z intervalu (-1,1)).
df2 = pd.DataFrame()
df2["správně"] = df["správně"]
df2["predikováno"] = df2["správně"].apply(lambda predikovano: predikovano + random.uniform(-1., 1.))
df2
Opět zorbrazme chyby:
df2_chyby, MSE_2, MAE_2, R2_2 = spocti_metriky(df2["správně"], df2["predikováno"])
pd.concat([df2, df2_chyby], axis="columns")
A vypišme si hodnoty metrik:
print(f"MSE = {MSE_2:.3f} (minule: {MSE})") # :.2f znamená float na dvě desetinná místa
print(f"MAE = {MAE_2:.3f} (minule: {MAE})")
print(f"R2 = {R2_2:.3f} (minule: {R2})")
Vidíme, že hodnoty MSE a MAE jsou teď výrazně menší než minule. To je proto, že "predikované" hodnoty jsou velmi blízko hodnotám skutečným. $R^2$ skóre vyšlo naopak vyšší (blíže jedné).
Pozn.: Pozor, nyní vyšla hodnota MAE vyšší než MSE, to je proto, že jednotlivé chyby jsou teď menší než jedna (mocnina je menší než absolutní hodnota).