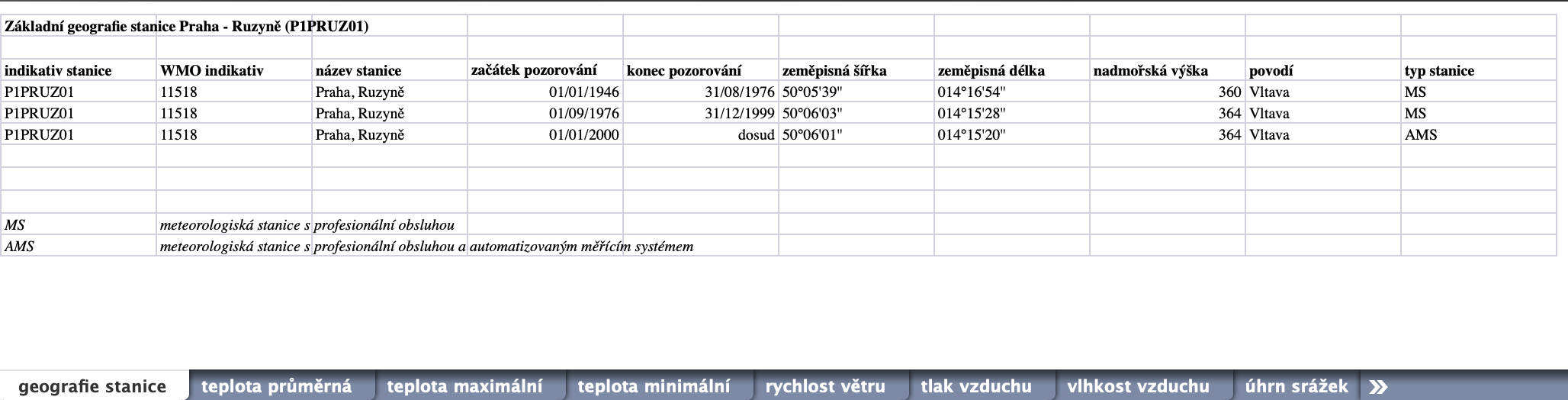
Explorativní analýza a statistika jedné proměnné
V této lekci se podíváme na základní nástroje a postupy, které se hodí pro analýzu jedné proměnné. Nebudeme se tedy zabývat vztahy a souvislostmi mezi více proměnnými - to bude předmětem mnohých dalších lekcí. Na pomoc si pro tento účel vezmeme především časové řady s údaji o počasí (teplota, tlak apod.). V práci nám bude významě pomáhat vizualizace.
Abychom s daty mohli efektivně pracovat, budeme muset data ještě transformovat a pročistit. To je (bohužel) běžnou součástí datové analýzy, protože zdrojová data jsou typicky ne zcela vhodně uspořádána a často obsahují i chyby. Při práci s časovými řadami využijeme bohaté možnosti pandas pro práci s časovými údaji.
Podíváme se na základy statistiky. Dozvíme se, jak pracovat s pojmy střední hodnota, standardní odchylka, medián, kvantil či kvartil. Naučíme se pracovat s histogramy, s boxploty a s distribuční funkcí.
V této lekci se naučíš:
- načítat data ze souborů ve formátu Excel,
- efektivně čistit a transformat data na "spořádaná data",
- základní statistiky jedné proměnné, včetně rozdělovací funkce,
- vizualizovat časové řady a jejich statistické vlastnosti.
Načtení knihoven
Budeme používat samozřejmě pandas, pro vizualizaci pak matplotlib a seaborn.
%matplotlib inline
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
Příprava dat
Načtení hrubých dat - počasí
Naší základní datovou sadou budou data o počasí, konkrétně v Praze - Ruzyni. Data poskytuje Českým hydrometeorologický ústav (ČHMÚ) ve formě Excel souborů, dostupných z http://portal.chmi.cz/historicka-data/pocasi/denni-data/data-ze-stanic-site-RBCN.
Možná překvapivě není úplně snadné dobrá a podrobná data získat. Ta nejkvalitnější jsou placená, navíc "Česká data o počasí patří k nejdražším". Jen nedávno soud nařídil poskytovat alespoň základní data zdarma, viz článek na irozhlas.
Takto vypadají náhledy dvou listů ze souboru P1PRUZ01.xls, který obsahuje historická data z meteorologických měření v Praze - Ruzyni. Data jsou poměrně nepěkně uspořádána. Ani v Excelu by se s těmito soubory nepracovalo dobře ...
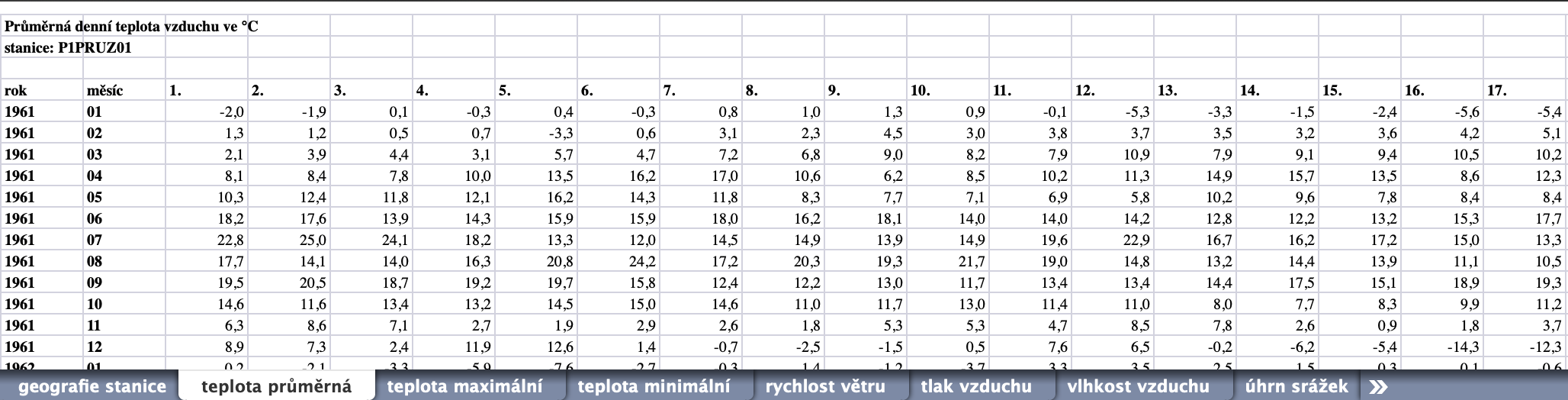
Samotné načtení souboru je poměrně snadné. Použijeme na to třídu ExcelFile, protože kromě načítání poskytuje také property sheet_names.
Často stačí (a je jednodušší) použít funkci read_excel. V dokumentaci si všimni velkého množství argumentů, které umožňují správně načíst všelijak formátované soubory a hodnoty v nich.
RUZYNE_DATA_FILENAME = "P1PRUZ01.xls"
RUZYNE_DATA_URL = "https://data4pydata.s3-eu-west-1.amazonaws.com/pyladies/P1PRUZ01.xls"
# stáhne data pokud ještě nejsou k dispozici
import os
import requests
def save_file_from_url(url, target_filename):
if not os.path.isfile(target_filename):
print("Stahuji data - počkej chvíli ...")
response = requests.get(url)
with open(target_filename, "wb") as out:
out.write(response.content)
print(f"Data jsou v souboru {target_filename}")
save_file_from_url(RUZYNE_DATA_URL, RUZYNE_DATA_FILENAME)
# otevření Excel souboru
excel_data_ruzyne = pd.ExcelFile(RUZYNE_DATA_FILENAME)
Zobrazíme si seznam listů v souboru.
excel_data_ruzyne.sheet_names
Zatím jsme žádná data nenačetli (nemáme žádný DataFrame s daty ze souboru). Data načte ve formě DataFrame až metoda parse.
# načti data z jednoho listu a zobraz prvních 5
teplota_prumerna = excel_data_ruzyne.parse("teplota průměrná")
teplota_prumerna.head(5)
Výsledek není přesně to, co bychom chtěli. Náprava je ale naštěstí jednoduchá - potřebujeme jen přeskočit první tři řádky. K tomu stačí přidat skiprows=3.
teplota_prumerna = excel_data_ruzyne.parse("teplota průměrná", skiprows=3)
teplota_prumerna.head(5)
Tohle vypadá už trochu lépe - řádky a sloupce jsou tak, jak bylo zamýšleno. Problémem ale je, že dny jsou jako sloupce. Už jen proto, že ne každý měsíc má 31 dní. Proto se v posledních třech sloupcích vyskytují nedefinované hodnoty neboli NaN (Not a Number).
Chybějící hodnoty se mohou vyskytnout i z jiných důvodů než "jen" kvůli nevhodnosti uspořádání dat. Např. mohl mít měřící přístroj závadu, data se poškodila apod. Pro chybějící hodnoty mohou být použity různé zkratky a symboly a právě proto existuje šikovný argument na_values.
Z mnoha dobrých důvodů, které samy/i uvidíte v praxi, je naším cílem dostat data do podoby tzv. tidy data, kdy řádky odpovídají jednotlivým pozorováním (měřením), názvy sloupců odpovídají veličinám.
Tady přijde vhod metoda melt. Ta slouží právě pro případy, kdy hodnoty jsou zakódované jako názvy sloupců. Takto vysvětlíme melt, že sloupce ["rok", "měsíc"] jsou už správně jako "veličiny", že v názvech zbývajících sloupců jsou hodnoty veličiny den a že hodnoty patří veličině teplota průměrná, což se použije pro pojmenování nového sloupce.
teplota_prumerna_tidy = teplota_prumerna.melt(
id_vars=["rok", "měsíc"], var_name="den", value_name="teplota průměrná"
)
teplota_prumerna_tidy.head(5)
V tomto případě bylo celkem jasné, že názvy sloupců jsou vlastně hodnoty nějaké veličiny. Někdy to může být více skryté, např. v případě kategorických proměnných. Třeba data z měření délky nohou můžeme dostat v tomto formátu:
leg_length = pd.DataFrame({"left": [81, 81.4], "right": [78.2, 78]})
leg_length
Úkol: Má leg_length podobu tidy data? Pokud ne, dokážeš tato data uspořádat správně? Nápovědná otázka: Lze stranu nohy považovat za (kategorickou) veličinu?
Vytvoření "správného" (časového) indexu
Téměř nikdy nechceme pracovat s oddělenými sloupci "rok", "měsíc" apod. Práci s časovými údaji a časovými řadami mají na starosti specializované třídy, především Timestamp a DatetimeIndex, pro rozdíly mezi časovými údaji pak Timedelta. Přehled najdeš v dokumentaci: Time series / date functionality. A věřte - není to jednoduchý problém. Časová algebra pracuje zároveň s desítkovou, šedesátkovou, dvanáctkovou, dvacetčtyřkovou, sedmičkovou, měsíční, kvartální, roční, ... algebrou. Do toho vstupují časové zóny, přestupné roky, letní čas, různé kalendáře a kdo ví co ještě.
Pojďme tedy vytvořit pro naši časovou řadu ten "správný" časový index. K tomu se často se hodí funkce to_datetime. Tato funkce umí převádět numerické nebo textové údaje (jednotlivě i celé řady) do toho správného Pandas typu pro práci s časovými údaji.
Pro nás se hodí, že umí pracovat i s daty, kde jsou v oddělených sloupcích roky, měsíce, dny atd. Ukážeme si to na na jednoduchém příkladu.
# příklad řady datumů v oddělených sloupcích
split_dates_example = pd.DataFrame(
{"year": [2015, 2016], "month": [2, 3], "day": [4, 5]}
)
split_dates_example
Funkce to_datetime nám z ukázkové tabulky vytvoří řadu (Series) typu datetime64[ns]. Tento (numpy) typ podporuje mnoho užitečných metod pro práci s časovými údaji, viz. Datetimes and Timedeltas. Údaj [ns] ukazuje na (výchozí) nanosekundovou přesnost.
pd.to_datetime(split_dates_example)
Aby to fungovalo na naše česká data, je potřeba jen přejmenovat sloupce "rok", "měsíc", "den" na "year", "month", "day". K tomu máme metodu rename, tak to pojďme vyzkoušet rovnou dohromady. Výsledek uložíme do nové proměnné datum.
datum = pd.to_datetime(
teplota_prumerna_tidy[["rok", "měsíc", "den"]].rename(
columns={"rok": "year", "měsíc": "month", "den": "day"}
),
)
Skoro - skončilo to poměrně logickou chybou (výjimkou) ValueError: cannot assemble the datetimes: day is out of range for month. Nepovedlo se (naštěstí) přesvědčit pandy, že všechny měsíce mají 31 dní :)
Pomocí errors="coerce" ale můžeme nařídit, aby se převedla všechna správná data a chybná data se označila jako NaN, resp. v tomto případě NaT - Not a Time.
datum = pd.to_datetime(
teplota_prumerna_tidy[["rok", "měsíc", "den"]].rename(
columns={"rok": "year", "měsíc": "month", "den": "day"}
),
errors="coerce",
)
datum
Pro úplnou informaci o čase bychom měli ještě přidat údaj o časové zóně. To nám umožní správně časy porovnávat, nebo třeba zachytit letní a zimní čas, což je často dosti svízelný problém. V našem případě denních dat to sice není zcela zásadní, v některých případech se to ale projevit může.
U časových údajů, které neobsahují časovou zónu, můžeme použít .dt.tz_localize. Pro konverzi časové zóny pak slouží .dt.tz_convert.
.dt je tzv. accessor object pro práci s časovými vlastnostmi dat.
datum_localized = datum.dt.tz_localize("Europe/Prague")
datum_localized
Určitě jste si všimli, že přibyl i údaj o čase, a samozřejmě o časové zóně a tím i o posunu od UTC. +01:00 znamená +1 hodina od UTC. U datumů je totiž koncept časové zóny ne úplně přirozený a proto Pandas přidal i čas (00:00:00). Jelikož je ale často význam denních dat nějaký souhrn za konkrétních 24 hodin (a někdy za 23 hodin a někdy za 25 hodin díky střídaní letního a zimního času), je lepší pracovat i konkrétním časem (začátkem dne). A to je i náš případ.
Teď už jen pomocí assign přidáme sloupec "datum". Můžeš ověřit, že následná analýza bude fungovat i s lokalizovaným časem datum_localized.
teplota_prumerna_tidy = teplota_prumerna_tidy.assign(datum=datum)
teplota_prumerna_tidy
Úkol: to_datetime dokáže pracovat i s řetězci, což se často hodí. Převeďte ladies_times na vohodný typ pro časové údaje, přiřaďte naši časovou zónu a poté pomocí tz_convert převeďte na UTC. Možná budete muset pandám vysvětlit, že v Česku jsou v datumech nejdříve dny, na rozdíl třeba od Ameriky. Naštěstí na to stačí jeden jednoduchý argument pro to_datetime.
ladies_times = ["15. 9. 2020 18:00", "22. 9. 2020 18:00", "29. 9. 2020 18:00"]
pandas_times = pd.to_datetime(___).___.___
Čištění dat
Co se stalo s nedefinovanými hodnotami? Zůstaly tam. Pojďme se podívat, jak to vlastně zjistit a co se s tím dá dělat.
Obecně máme tři základní možnosti.
Nedělat nic, tj. nechat chybějící data chybět. To je možná překvapivě často dobrá volba, protože mnoho funkcí si s chybějícími daty poradí správně. To je rozdíl oproti
numpy, kde funkce typickyNaNy nemají rády. Často existují varianty funkcí (např.numpy.mean->numpy.nanmean), kteréNaNy berou jako chybějící data.Pozorování (tj. řádky, protože máme tidy data) s chybějícími záznamy vynechat. K tomu slouží metoda
dropna.Chybějící data nahradit nějakou vhodnou hodnotou. Co jsou vhodné hodnoty, záleží na povaze dat a na tom, co s daty dále děláme. Někdy je vhodné nahradit chybějící hodnoty nějakou "typickou" hodnotou, třeba průměrem. Pro časové řady je většinou logičtější nahradit hodnotou z okolí (předchozí nebo následující). O nahrazování typickými hodnotami (angl. imputation) se dočteš https://scikit-learn.org/stable/modules/impute.html a možná dozvíš víc i později. K nahrazování hodnotami z okolí pak slouží metoda
fillna.
Pro naše účely se bude nejvíce hodit vynechat chybějící záznamy, které vznikly nehezkým uspořádáním Excel souboru.
Nejprve bychom ale měli zjistit, kde přesně ty chybějící hodnoty jsou. Metoda isna nám dokáže "najít" nedefinované hodnoty:
teplota_prumerna_tidy.isna()
Použití sum na True a False je užitečný trik, True se počítá jako 1, False jako 0.
teplota_prumerna_tidy.isna().sum()
Vidíme tedy, že ve sloupcích s teplotou a datumem je 392 nedefinovaných hodnot.
Můžeme si také zobrazit výběr řádků, kde je alespoň nějaký NaN. Jistě si pamatuješ, že indexovat lze pomocí řady typu bool. Drobný problém je, že máme těch řad víc - pro každý sloupec jednu. Můžeme ale použít .any(axis=1), abychom vybrali řádky, kde je alespoň nějaký NaN:
teplota_prumerna_tidy.loc[teplota_prumerna_tidy.isna().any(axis=1)].sample(5)
Způsobem, jak získat naopak počet nechybějících (platných) hodnot, je metoda count
teplota_prumerna_tidy.count()
Otázka: Co vrátí teplota_prumerna_tidy.isna().count()?
Teď už ale ta chybějící data chceme odstranit. Podívejme se na jednoduchém příkladu, jak funguje dropna.
# příklad dat s chybějícími hodnotami
example_with_nan = pd.DataFrame({"A": [1, 2, np.nan, 4, 5], "B": [1, 2, 3, np.nan, 5]})
example_with_nan
Po dropna zbudou pouze řádky bez chybějících hodnot.
example_with_nan.dropna()
Tohle přesně potřebujeme na naše data, která teď vyčistíme od nedefinovaných hodnot:
teplota_prumerna_tidy_clean = teplota_prumerna_tidy.dropna()
Úkol: Využijte toho, že teplota není definovaná v neexistující dny. Použijte vhodně dropna v sestrojení datumů tak, abychom nemuseli použít errors="coerce" pro to_datetime.
# přidejte dropna
pd.to_datetime(
teplota_prumerna_tidy[["rok", "měsíc", "den"]].rename(
columns={"rok": "year", "měsíc": "month", "den": "day"}
),
)
Úkol: Z proměnné teplota_prumerna_tidy_clean vytvořte teplota_prumerna_tidy_clean_indexed se sloupcem datum jako indexem a bez sloupců rok, měsíc a den. Můžete použít metodu drop nebo indexování s názvy sloupců.
teplota_prumerna_tidy_clean_indexed = ___
Vše dohromady
Parsování celého souboru, tj. jeho načtení a převedení do požadované formy Pandas DataFrame, máme teď hotové. Pro další generace (a naše použití) na to definujeme funkci. V rámci této funkce také vyhodíme sloupce rok, měsíc a den, sloupec datum použijeme jako index a data podle datumu setřídíme. Přidali jsme ještě jméno listu jako vstupní parameter, což se bude hodit hned vzápětí pro načítání všech listů do jednoho DataFrame.
def extract_and_clean_chmi_excel_sheet(excel_data, sheet_name):
"""Parse ČHMÚ historical meteo excel data"""
# načti list z excel souboru a převeď na tidy data formát
data_tidy = (
excel_data.parse(sheet_name, skiprows=3)
.melt(id_vars=["rok", "měsíc"], var_name="den", value_name=sheet_name)
.dropna()
)
# vytvoř časovou řadu datumů
datum = pd.to_datetime(
data_tidy[["rok", "měsíc", "den"]].rename(
columns={"rok": "year", "měsíc": "month", "den": "day"}
)
)
# přidej sloupec datum jako index a odstraň den, měsíc, rok a vrať setříděný výsledek
return (
data_tidy.assign(datum=datum)
.set_index("datum")
.drop(columns=["rok", "měsíc", "den"])
.sort_index()
)
A teď už si můžeme načíst všechna data z Ruzyně tak, jak se nám budou hodit pro analýzu.
# otevři Excel soubor
excel_data_ruzyne = pd.ExcelFile("P1PRUZ01.xls")
# načti všechny listy kromě prvního
extracted_sheets = (
extract_and_clean_chmi_excel_sheet(excel_data_ruzyne, sheet_name)
for sheet_name in excel_data_ruzyne.sheet_names[1:]
)
# spoj všechny listy do jednoho DataFrame
ruzyne_tidy = pd.concat(extracted_sheets, axis=1)
U použití concat je důležité, že všecha data mají stejný index. axis=1 říká, že se mají skládat sloupce vedle sebe. Výchozí axis=0 by spojovala data pod sebe a nedopadlo by to úplně dobře (můžeš vyzkoušet :). Detailněji si o spojování tabulek budeme povídat příště.
Prohlédneme si výslednou tabulku ruzyne_tidy.
ruzyne_tidy
Indexování a výběr intervalů
Data, která jsme načetli a vyčistili, tvoří vlastně několik časových řad v jednotlivých sloupcích tabulky ruzyne_tidy. Granularita (nebo frekvence či časové rozlišení) je jeden den.
Pomocí to_period() bychom mohli datový typ indexu převést i na period[D]. To může zrychlit některé operace, pro naše použití to ale není nezbytné.
ruzyne_tidy.index.to_period()
Už jsme si ukazovali indexování (výběr intervalu) pomocí .loc. U časových řad to funguje samozřejmě také. Pozor na to, že .loc vrací data včetně horní meze, na rozdíl od indexování listů nebo numpy polí.
Konkrétní období můžeme vybrat třeba takto:
ruzyne_tidy.loc[pd.Timestamp(2017, 12, 24) : pd.Timestamp(2018, 1, 1)]
Atributy časových proměnných
Časové proměnné typu DatetimeIndex poskytují velice užitečnou sadu atributů vracející
- části časového údaje, např.
.yearvrátí pouze rok,.monthměsíc apod., - relativní informace , např.
.weekdaynebo.weekofyear - kalendářní vlastnosti jako
is_quarter_startnebois_year_end, které by bylo poměrně náročné zjišťovat numericky.
Pokud se jedná o sloupec, je potřeba před atribut vložit ještě .dt accessor.
ruzyne_tidy.index.year
Můžeme tak vybrat jeden celý rok např. takto:
ruzyne_tidy.loc[ruzyne_tidy.index.year == 2018]
Nebo můžeme získat data pro všechny dny před rokem 1989, které jsou začátky kvartálů a zároveň to jsou pondělky.
ruzyne_tidy.loc[
ruzyne_tidy.index.is_quarter_start
& (ruzyne_tidy.index.weekday == 0)
& (ruzyne_tidy.index.year < 1989)
]
Úkol: Nejstarší tag Pandas na https://github.com/pandas-dev/pandas je verze 0.3.0 z 20. února 2011. Jaké bylo v ten den v Praze - Ruzyni počasi?
Úkol: Jaká byla průměrná teplota první (a jedinou) neděli v roce 2010, která byla zároveň začátkem měsíce? Pokud máte řešení a čas, zkuste vymyslet aternativní způsob(y).
ruzyne_tidy.loc[
___
& (___)
& (___),
"teplota průměrná",
]
Základní vizualizace
Vykreslíme si naše data co nejjednoduššími způsoby, jaké nám pandy nabízí. Zkusme třeba rovnou .plot()
ruzyne_tidy.plot();
Tam toho moc vidět není. Jedním z problémů je různá škála veličin. A také bychom si graf mohli trochu zvětšit.
ruzyne_tidy.plot(subplots=True, figsize=(12, 9));
Tohle už je trochu užitečné, něco málo na grafu vidět je. Výchozí čárový (line) graf je pro časové řady obvykle vhodný.
Pomocí argumentu layout můžeme podgrafy uspořádat do více sloupců. Pokud navíc vybereme kratší časové období, dostaneme už celkem srozumitelný výsledek.
ruzyne_tidy[ruzyne_tidy.index.year == 2018].plot(
subplots=True, layout=(3, 3), figsize=(12, 9)
);
I tady je ale dat poměrně hodně a na grafech vidíme spoustu rozptylu - hodnoty skáčou rychle nahoru / dolů. V takovém případě je na čase vzít si na pomoc statistiku!
Trocha statistiky - opravdu jen základní
Není cílem tohoto kurzu (a ani v jeho možnostech) podrobně a rigorózně učit statistiku ("Statistika nuda je..."). Jednoduché základy, které zvládají i 🐼🐼🐼, spolu jistě zvládneme a přesvědčíme se, že jsou i užite ("...má však cenné údaje...")čné.
Pokud se budeš chtít dozvědět víc, koukni třeba na https://www.poritz.net/jonathan/share/ldlos.pdf, nebo na http://greenteapress.com/thinkstats2/thinkstats2.pdf nebo třeba i na Bayesovskou statistiku http://www.greenteapress.com/thinkbayes/thinkbayes.pdf.
Metoda DataFrame.describe je jednoduchou volbou pro získání základních statistik celé tabulky.
ruzyne_tidy.describe()
Pro každý sloupec vidíme několik souhrnných (statistických údajů).
countudává počet hodnot.meanje střední hodnota, vypočítaná jako aritmetický průměr.stdje směrodatná odchylka, která ukazuje rozptyl dat - jak moc můžeme očekávat, že se data v souboru budou lišit od střední hodnoty.minamaxjsou nejmenší a největší hodnoty ve sloupci.- Procenta označují kvantily,
25%a75%je hodnota prvního a třetího "kvartilu". Pokud bychom sloupec seřadili podle podle velikosti, bude čtvrtina dat menší než hodnota prvního kvartilu a čtvrtina dat bude větší než hodnota třetího kvartilu. Konkrétně čtvrtina všech dní v našich datech měla minimální teplotu menší než -0.7 °C a čtvrtina dní zase měla maximální teplotu větší než 20.5 °C. 50%se označuje jako medián - polovina dat je menší než medián (a ta druhá polovina je samozřejmě zase větší než medián).
Za chvilku si ještě ukážeme, jak tyto hodnoty souvisi s distribuční funkcí a vše ti bude hned jasnější :)
describe můžeme samozřejmě použít i na nějakou podmožinu dat. Takto třeba vypadá statistika počasí v Ruzyni v lednu.
ruzyne_tidy[ruzyne_tidy.index.month == 1].describe()
Statistické rozdělení
Pojďme zkusit pojmy kolem pravděpodobnosti, jako třeba rozdělovací funkce nebo hustota pravděpodobnosti, jejichž formální definice a vlastnosti lze najít v knihách (např. v těch uvedených výše) nebo na wikipedii, objevovat a zkoumat spíš názorně a intuitivně.
Jedním ze základních a nesmírně užitečných nástrojů na vizualizaci souboru dat je histogram. Zjednodušeně řečeno, histogram vytvoří chlívečky podle velikosti dat - do každého chlívečku patří data v nějakém intervalu od - do. Počet hodnot, které ze souboru dat spadnou do daného chlívečku, určuje velikost (výšku) chlívečku.
Histogram zobrazíme pomocí .plot.hist()
ruzyne_tidy["tlak vzduchu"].plot.hist(edgecolor="black");
Histogram nám říká, že někde v rozmezí 971 - 978 je nejvíce hodnot (skoro 8000). Okolní chlívečky mají o něco menší velikost, 964 - 971 cca 5000, 978 - 985 cca 4000. Na okrajích jsou jen nízké chlívečky, jakési ocasy.
Přemýšlej - kdybychom si vybrali náhodně jeden den.
- Z kterého (jednoho) z chlívečků v grafu bude nejčastěji ležet tlak?
- Jakých 5 chlívečků bys vybrala, abys měla opravdu hodně velkou šanci, že tlak ve vybraném dni bude v jednom z těchto chlívečků?
Pokud dokážeš na otázky odpovědět, tak už vlastně víš, že histogram udává hustotu pravděpodobnosti a že tahle hustota se dá sčítat, čímž se dostane kumulovaná pravděpodobnost, neboli také distribuční funkce.
Definice je vlastně docela jednoduchá (zdroj wikipedia):
Distribuční funkce, funkce rozdělení (pravděpodobnosti) nebo (spíše lidově) (zleva) kumulovaná pravděpodobnost (anglicky Cumulative Distribution Function, CDF) je funkce, která udává pravděpodobnost, že hodnota náhodné proměnné je menší než zadaná hodnota.
Hustota pravděpodobnosti vyjadřuje, kolik "pravděpodobnosti" přibude na daném intervalu, neboli o kolik se změní distrubuční funkce. Matematicky je hustota pravděpodobnosti derivací distribuční funkce.
Poměrně důležitým parametrem u histogramu je počet chlívků. Když jich je málo, může zaniknout důležitá informace, moc chlívků může zase vnést velký šum.
Pro naše data vypadá histogram s třiceti chlívky celkem rozumně.
ruzyne_tidy["tlak vzduchu"].plot.hist(bins=30, figsize=(12, 6), edgecolor="black");
Na vlastní nebezpečí můžete na tvoření histogramů použít physt Honzy Pipka. Přidává pár zajímavých vlastností a často usnadní práci.
# physt možná nemáte nainstalovaný - stačí odkomentovat
# %pip install physt
import physt
histogram = physt.h1(ruzyne_tidy["tlak vzduchu"], "fixed_width", bin_width=5)
histogram.plot(edgecolor="black", show_values=True, show_stats=True);
Argument cumulative=True nám pak zobrazí postupný (kumulativní) součet velikosti chlívků. Použijeme ještě density=True, abychom zobrazili distribuční funkci. Takto nám graf říká, jaká je pravděpodobnost (hodnota na vertikální ose), že tlak bude menší než daná hodnota (na horizontální ose).
V grafu jsou ještě přidané svislé čáry pro střední hodnotu (černá), medián (červená) a 25% a 75% kvantily (červené přerušované).
ax = ruzyne_tidy["tlak vzduchu"].plot.hist(
bins=30, figsize=(12, 6), cumulative=True, density=True, grid=True
)
ax.set_yticks(np.arange(0, 1.1, 0.25))
ax.axvline(ruzyne_tidy["tlak vzduchu"].mean(), color="k")
ax.axvline(ruzyne_tidy["tlak vzduchu"].median(), color="r")
ax.axvline(ruzyne_tidy["tlak vzduchu"].quantile(0.25), color="r", ls="--")
ax.axvline(ruzyne_tidy["tlak vzduchu"].quantile(0.75), color="r", ls="--")
Podívejme se, jak vypadají histogramy všech devíti veličin.
ruzyne_tidy.hist(figsize=(12, 9), bins=30);
ruzyne_tidy.hist(figsize=(12, 9), bins=30, cumulative=True, density=True);
Je poměrně zajímavé a příhodné, že dostáváme poměrně hezkou paletu různých typu rozdělovací funkce. Tlak vzduchu má přibližně normální (Gaussovo) rozdělení. O tom jste možná slyšeli, protože se vyskutuje a používá poměrně často (někdy až příliš často). U teploty je zajímavé, že má tzv. bi-modální rozdělení - na histogramu jsou dvě maxima. U dalších veličin se můžeme zamyslet, která z mnoha známých distribucí by se na jejich popis více či méně hodila. Logaritmicko-normální na na rychlost větru? Nějaká exponenciální (nebo obecně gamma) distribuce výšky sněhu, úhrnu srážek a možná slunečního svitu? Toto ponechejme na nějaký podrobnější kurz statistiky, meteorologie či klimatologie :)
Různorodé distribuční funkce nám ale umožní ukázat některé vlastnosti střední hodnoty a mediánu. To jsou (společně s módy, tedy maximy hustoty pravděpodobnosti) ukazatele centrální tendence souboru dat. Medián a střední hodnota se poměrně často neliší a u "hezkých" (symetrických) distribucí, jako je normální rozdělení, jsou totožné. Lišit se budou zejména tehdy, když je distribuce sešikmená (angl. skewed) nebo pokud jsou v datech odlehlé hodnoty, spíše známé pod anglickým výrazem outliers.
Zabalíme do funkce vykreslovaní histogramu spolu se střední hodnotou a kvantily, které jsme použili již dříve. Poté použijeme velice užitečnou knihovnu seaborn na vykreslení histogramů pro jednotlivé veličiny.
def hist_plot_with_extras(data, bins=30, cumulative=False, density=False, **kwargs):
"""Plot histogram with mean and quantiles"""
ax = kwargs.pop("ax", plt.gca())
ax.hist(data, bins=bins, cumulative=cumulative, density=density, **kwargs)
ax.grid(True)
if density:
ax.set_yticks(np.arange(0, 1.1, 0.25))
ax.axvline(data.mean(), color="k")
ax.axvline(data.median(), color="r")
ax.axvline(data.quantile(0.25), color="r", ls="--")
ax.axvline(data.quantile(0.75), color="r", ls="--")
return ax
Všimněte si použití .melt() - seaborn totiž očekává data v jednom sloupci, jednotlivé grafy pak tvoří na základě hodnoty jiného sloupce. Vytvořili jsme vlastně kategorickou proměnnou "value".
Teď můžeme použít FacetGrid, který vytváří sadu grafů, rozdělených do mřížky podle nějaké vlastnosti dat (kategorie).
grid = sns.FacetGrid(
ruzyne_tidy.melt(),
col="variable",
col_wrap=2,
sharey=False,
sharex=False,
aspect=2,
)
grid.map(hist_plot_with_extras, "value");
Kromě histogramu se velice často používá pro zobrazení distribuce tzv. boxplot. "Krabička" (obdélník) uprostřed vymezuje oblast mezi prvním a třetím kvartilem (Q1 a Q3), dělicí čára odpovídá mediánu, a "vousy" (anglicky whiskers) značí rozsah dat. Standardně je to poslední bod, který je menší / větší než 1,5násobek "inter-quartile range" IQR, IQR = Q3 - Q1. Tento rozsah se obvykle považuje za mez pro odlehlé hodnoty, které jsou pak v boxplotu vyznačeny jako symboly (kosočtverce v našem případě).
grid = sns.FacetGrid(
ruzyne_tidy.melt(),
col="variable",
col_wrap=2,
sharey=False,
sharex=False,
aspect=2,
)
grid.map(sns.boxplot, "value");
Seaborn se často dá použít velice jednoduše, pokud zobrazujeme jednu veličinu, a někdy stráví i "wide-format" data. U našich dat můžeme takto porovnat průměrnou, minimální a maximální teplotu. Na pomoc si vezmeme catplot, který vytváří graf (nebo i sadu grafů) různých typů (boxplot nebo třeba violinplot) z dat obsahujících jednu či více kategorických proměnných.
sns.catplot(
data=ruzyne_tidy[["teplota průměrná", "teplota maximální", "teplota minimální"]],
orient="h",
kind="box",
aspect=2,
);
Úkol: Doplňte pomocné sloupce season a significant_precipitation (jistě uhádnete jakého pandas-typu budou :). První definuje roční období (jen jednoduše podle kalendářních měsíců), drůhý označuje dny, kdy byly srážky vyšší než v 90 % všech dní v našich datech (můžete zkusit i jiný limit).
- Porovnejte numericky základní statistiky celého datasetu a podmnožiny, kdy výrazně pršelo nebo sněžilo. Zvyšují v průměru srážky teplotu? A co maximální nebo minimální? A jak je to se standardní odchylkou?
- Použijte
sns.catplotpro vizuální srovnání distribučních funkcí pro jednotlivá roční období a dny s málo / hodně srážkami.
season = ruzyne_tidy.index.___.map({
1: "zima",
2: "zima",
3: "jaro",
...
})
significant_precipitation = ruzyne_tidy["úhrn srážek"] > ruzyne_tidy[___].quantile(___)
# úkol - jednoduché srovnání statistik pomocí rozdílu
(ruzyne_tidy.loc[___]
.describe()
) - \
ruzyne_tidy.___()
# úkol - vizuální srovnání statistik
sns.catplot(
data=ruzyne_tidy.assign(
significant_precipitation=___,
season=___,
),
kind="box",
aspect=2,
hue=___,
y=___,
x=___,
);
Práce s časovou řadou
Pojďme trochu zkombinovat statistiku a práci s časovou řadou. Zajímalo by vás, jak moc byl který rok teplý či studený? Pomocí resample můžeme změnit rozlišení dat na jiné období, např. jeden rok.
ruzyne_yearly = ruzyne_tidy.resample("1Y")
Co že jsme to vlastně vytvořili?
ruzyne_yearly
Dostali jsme instanci třídy DatetimeIndexResampler. To zní logicky, ale kde jsou data? Ta zatím nejsou, protože jsme ještě pandám neřekli, jak vlastně mají ze všech těch denních údajů v rámci jednoho roku vytvořit ta roční data. Neboli, jak data agregovat.
Ze statistiky víme, že jedním z ukazatelů může být střední hodnota. Zkusíme vypočítat průměrnou "teplotu průměrnou" (není to překlep) a rovnou vykreslit.
ruzyne_yearly["teplota průměrná"].mean().plot();
Trochu podobnou operací jako resampling je rolování. To spočívá v plynulém posouvání "okna", které slouží pro (vážený) výběr dat a následné aplikaci agregační funkce (jako u resample). Pojďme pomocí rolling vytvořit podobný pohled na roční průměrnou teplotu. Rozdíl oproti resample je v tom, že dostaneme pro každý den jednu hodnotu, nikoli jen jednu hodnotu pro celý rok. A také už nemůžeme použít interval "1Y", protože jeden (kalendářní) rok není dobře definovaný interval díky přestupným rokům.
ruzyne_tidy["teplota průměrná"].rolling("365.25D", min_periods=365).mean().plot();
Pro podrobnější přehled práce s časovými řadami se podívejta např. na https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html nebo třeba na hezký článek s podobnými daty https://www.dataquest.io/blog/tutorial-time-series-analysis-with-pandas/.
Úkol: Navrhněte vhodnou agregaci pro maximální teplotu (ne průměr) a vykreslete.
ruzyne_yearly[___].___().___();
Úkol: Převzorkujte údaje za rok 2018 po měsících. Jaký měsíc měl nejvíc srážek, tj. za jaký byl součet sloupce "úhrn srážek" nejvyšší?
# doplňte nebo vyřešte po svém :)
ruzyne_tidy.loc[___ == 2018, "úhrn srážek"].___(
"1M"
).___().___(ascending=False).index[___].___