Analýza hlavních komponent (PCA)
...a jiné metody průzkumu dat a redukce počtu dimenzí
Co se naučíte
Analýza hlavních komponent (anglicky “principal component analysis” neboli PCA) je metoda na snížení počtu dimenzí mnohorozměrných dat. To se může hodit z hlediska vizualizace nebo kvůli úspoře času/paměti při strojovém učení.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
%matplotlib inline
sns.set_style('whitegrid')
Jak porovnat babičce víno ve spíži?
Data níže obsahují 13 různých charakteristik 178 italských vín. Představte si, že chcete tato vína vykreslit jako body do jednoho grafu. Případně si představte, že vás babička poprosila, abyste je vyrovnali do polic tak, aby "podobná" vína byla u sebe a "různá" vína co nejdál od sebe. Jak něco takového uděláte?
from sklearn.datasets import load_wine
wine = load_wine()
wine_df = pd.DataFrame(wine.data, columns=wine.feature_names)
print(wine_df.shape)
wine_df.head()
Jedna možnost je vybrat si dvojici dvou vlastností, která je zásadní pro vaše data. Ale co když se ve víně nevyznáte? Můžete pochopitelně vykreslit grafy všech možných dvojic.
sns.pairplot(wine_df);
plt.figure(figsize=(20,10))
sns.heatmap(wine_df.corr(), annot=True);
Jak vidíme, mnoho charakteristik je korelovaných (např. total_phenols a flavanoids). PCA umožňuje převést mnoho charakteristik (sloupců) na několik málo, které a) jsou nezávislé b) zachycují maximum informace (variability) v datech.
Protože obrazovky a stěny ve spíži obvykle bývají dvourozměrné, budeme dále (nebude-li řečeno jinak) zjednodušovat z X charakteristik na dvě, abychom tyto potom mohli zakreslit do grafu na osu $x$ a $y$. Podívejme se, jak to dopadne pro náši datovou sadu vín.
PCA graf
# Tento blok znormalizuje sloupečky v tabulce, aby měly průměr nula a rozptyl jedna
# Pokud to neuděláte, bude hrát roli v jakých jednotkách slooupec je
scaler = StandardScaler()
wine_df_scaled = scaler.fit_transform(wine_df)
# Tento blok spočte PCA souřadnice (volíme zjednodušení na dvě komponenty)
pca = PCA(n_components=2)
wine_pca = pd.DataFrame(pca.fit_transform(wine_df_scaled), columns=['PCA1', 'PCA2'])
wine_pca
# A tento je zakreslí do grafu
sns.scatterplot(wine_pca.PCA1, y=wine_pca.PCA2);
Splnili jsme úkol, bude babička spokojená? Jsou podobná vína zakreslená poblíž sebe?
K vínům lze v naší databázi dohledat ještě jednu informaci - vína patří do jedné ze tří kategorií (barva vína?). A skutečně, pokud si body na PCA grafu obarvíme podle kategorie vína, jasně vidíme tři shluky.
sns.scatterplot(wine_pca.PCA1, y=wine_pca.PCA2, hue=wine.target_names[wine.target]);
Podíl zachycené variability
PCA umožňuje též kvantifikovat, kolik procent variability je v prvních dvou PCA komponentách zachyceno.
pca.explained_variance_ratio_
Cvičení 1: Kosatce
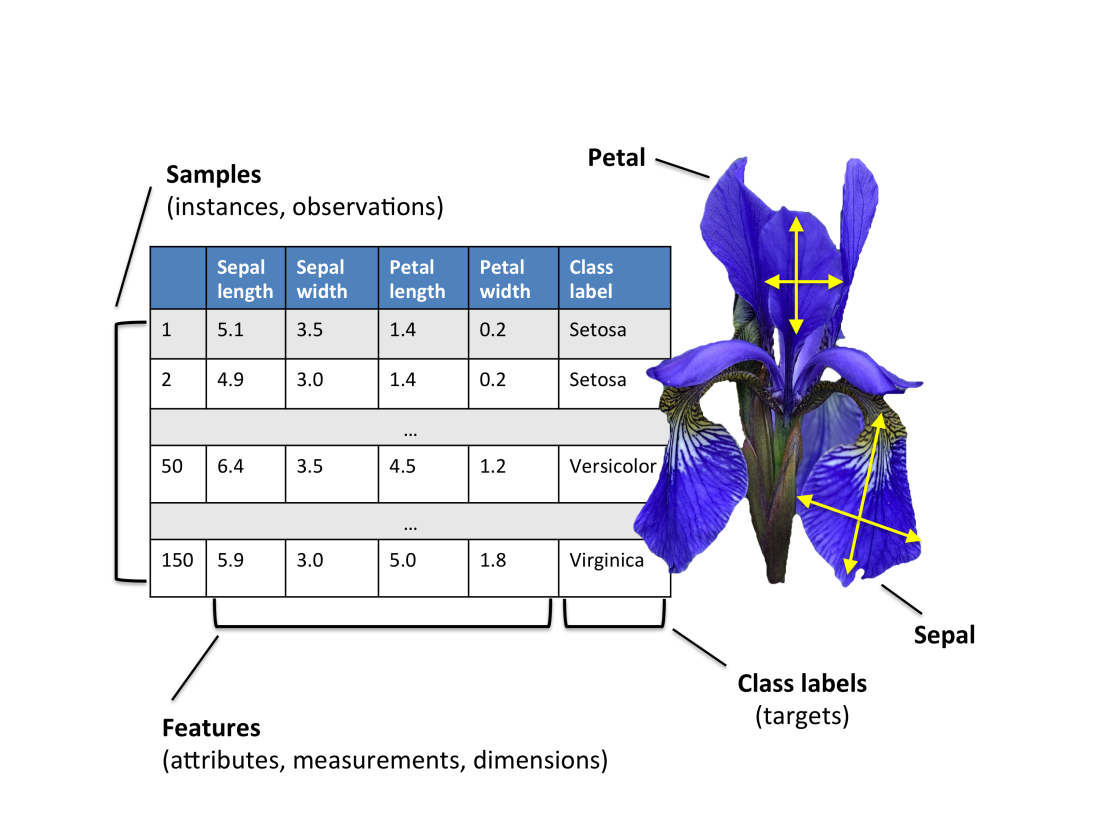
Možná už jste viděli Fisherova slavná data o kosatcích (anglicky iris). Připomeňme, že se jedná o 50 rostlin z 3 různých druhů kosatců a na každé bylo provedeno měření 4 charakteristik květu.
from sklearn.datasets import load_iris
iris = load_iris()
col_names = list(iris.feature_names)
iris_df = pd.DataFrame(iris.data, columns=col_names)
iris_df.head()
sns.heatmap(iris_df.corr(), annot=True);
Zredukujte tyto čtyři charakteristiky na dvě PCA, spočtěte množství vysvětlené variability a vykreslete vše do scatterplotu, který obarvíte podle druhu kosatce (v proměnné iris.target_names[iris.target]). Je na PCA grafu vidět rozdíl mezi druhy kosatců?
# sem napište řešení
Breast Cancer Wisconsin Dataset
Data z klinických měření ohledně rakoviny prsu z Wisconsinské univerzity. Celkem máme 569 pacientů a u každého z nich 31 veličin ohodnocujících FNA snímek prsní tkáně a informaci, zda-li byl nádor zhoubný (maligní) či nezhoubný (benigní).
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
col_names = list(cancer.feature_names)
col_names.append('target')
cancer_df = pd.DataFrame(np.c_[cancer.data, cancer.target], columns=col_names)
print(cancer_df.shape)
print(cancer.target_names)
cancer_df.head()
Začněme stejně jako v minulém případě pohledem párovými grafy, které si tentokrát obarvíme dle typu nádoru.
sns.pairplot(cancer_df, hue='target', vars=['mean radius', 'mean texture', 'mean perimeter', 'mean area',
'mean smoothness', 'mean compactness', 'mean concavity',
'mean concave points', 'mean symmetry', 'mean fractal dimension']);
plt.figure(figsize=(20,10))
sns.heatmap(cancer_df.drop(columns="target").corr(), annot=True);
Na první pohled vidíme, že některé charakteristiky nesou více informace než jiné.
plt.figure(figsize=(10, 8))
sns.scatterplot(x = 'mean area', y = 'mean smoothness', hue = 'target', data = cancer_df)
Spočítejme tedy nyní PCA komponenty, jejich podíl na variabilitě a nakresleme PCA graf.
scaler = StandardScaler()
scaler.fit(cancer_df.drop('target', axis=1))
scaled_data = scaler.transform(cancer_df.drop('target', axis=1))
pd.DataFrame(scaled_data).head()
pca = PCA(n_components=2)
cancer_pca = pd.DataFrame(pca.fit_transform(scaled_data), columns=['PCA1', 'PCA2'])
cancer_pca
pca.explained_variance_ratio_
plt.figure(figsize=(13,7))
sns.scatterplot(cancer_pca.PCA1, y=cancer_pca.PCA2,
hue=cancer.target_names[cancer.target],
)
plt.xlabel('PCA1 (44%)')
plt.ylabel('PCA2 (19%)');
Na PCA grafu je vidět několik oranžových (benigních) teček uprostřed modré (maligní) oblasti. Možná by bylo dobré podívat se na tyto pacienty podrobněji. Ale na jak zjistíme, kolikátému řádku bod odpovídá? Potřebujeme interaktivní graf!
Interaktivní PCA graf
import plotly.express as px
# V našich datech není Patient ID, tak si nějaké vytvoříme
cancer_df['patient'] = ['Patient' + str(i) for i in range(cancer_df.shape[0])]
cancer_df['patient']
# naucse.python.cz neumí zobrazit interaktivní graf, proto je níže zakomentovaný
fig = px.scatter(x=cancer_pca.PCA1, y=cancer_pca.PCA2, color=cancer.target_names[cancer.target],
hover_name = cancer_df['patient'])
#fig.show() # zrušte komentář pro nakreslení obrázku
Interpretace koeficientů
Aniž bychom příliš zabíhali do matematické podstaty PCA, každá naše uměle vytvořená komponenta je ve skutečnosti lineární kombinací jendotlivých charakteristik (po normalizaci), tedy např.
$$\texttt{PCA}_1 = \beta_0 + \beta_1 \texttt{Vlastnost(1)} + \beta_2 \texttt{Vlastnost(2)} + \cdots + \beta_k * \texttt{Vlastnost(k)}$$
Pokud jsme sloupce normalizovali pomocí StandardScaler, můžeme velikost koeficientů (v absolutní hodnotě) do jisté míry interpretovat jako jak moc se daná vlastnost na PCA komponentě podílí. Buďte však v této interpretaci opatrní (je snadné vidět v datech něco, co tam ve skutečnosti není).
loadings = pd.DataFrame(pca.components_.T, index=cancer_df.columns[:-2], columns=cancer_pca.columns)
loadings.sort_values('PCA1', ascending=False).head(n=10)
U části kódu v této části jsme se inspirovali v https://www.kaggle.com/faressayah/support-vector-machine-pca-tutorial. Kaggle je nejen soutěžní server, ale též velmi dobrý zdroj inspirace a návodů. Můžete se zde zkusit podívat na jiné techniky, které znáte z tohoto kurzu.
Cvičení 2: Vliv stárnutí na expresi proteinů v ledvinách
Pro druhé cvičení využijeme měření exprese proteinů z myších ledvin. Celkem máme 188 myší, které se liší pohlavím (samci, samice), zařazením do skupiny (generace, G8-G12) a věkem (6, 12 či 18 měsíců). Více informací o experimentu naleznete na https://ytakemon.github.io/TheAgingKidney/analysis.html. Názvy proteinů byly anonymizovány.
Na základě proteinové exprese nakreslete PCA graf a rozhodněte, jestli první dvě komponenty odpovídají nějaké informaci, kterou v záznamech máte (pohlaví, skupina, věk). Pokud vám zbyde čas, pokuste se nakreslit interaktivní graf.
url_protein_expr = 'http://github.com/simecek/naucse.python.cz/blob/master/lessons/pydata/pca/static/protein_expr.zip?raw=true'
protein_expr = pd.read_csv(url_protein_expr, compression="zip")
print(protein_expr.shape)
protein_expr.head()
# sem napište řešení
Na závěr si ukažme dva trochu zvláštnější případy použití:
Číslice
Ručně psaných 1797 číslic od 43 lidí, zmenšených do rastru 8x8, intenzita jasu od 0 do 16. Stejně jako většina našich dat pochází z UCI ML Repository.
Podívejme se na jednu konkrétní číslici, jak vypadá její číselná reprezentace a její obrázek.
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt
digits = load_digits()
#velikost dat
print(digits.data.shape)
# 42. číslice jako list
print(digits.images[42])
# 42. číslice jako obrázek
plt.gray()
plt.matshow(digits.images[42].reshape(8,8));
Data si převedeme ta tabulku o 1797 řádcích a 64 sloupcích (a ověříme si, že 42. řádek je správně).
digits.images[42].reshape(1,64)
digits_df = digits.images.reshape(1797,64)
print(digits_df.shape)
digits_df[42,:]
A nakreslíme si klasický PCA graf z prvních dvou komponent (povšimněte si, že nezávisí na tom, kolik n_components zvolíme).
# zkuste změnit počet komponent n_components a podívejte se, co se stane
n_components = 5
pca = PCA(n_components=n_components)
column_names = ["PCA" + str(i) for i in range(1,n_components+1)]
pca.fit(digits.images.reshape(1797,64))
digits_pca = pd.DataFrame(pca.transform(digits_df), columns=column_names)
digits_pca
plt.figure(figsize=(10,10))
sns.scatterplot(digits_pca.PCA1, y=digits_pca.PCA2,
hue=digits.target_names[digits.target], legend='full',
palette=sns.color_palette());
Inverzní transformace
PCA můžeme chápat i jako formu komprese dat, pro převod z prostoru PCA zpět slouží metoda inverse_transform. Zkuste měnit počet komponent a dívejte se, jak se mění podoba rekonstruované číslice 1.
digits_from_pca = pca.inverse_transform(digits_pca)
digits_from_pca
pca.explained_variance_ratio_, pca.explained_variance_ratio_.sum()
plt.matshow(digits_from_pca[42].reshape(8,8));
t-SNE
t-SNE (T-distributed Stochastic Neighbor Embedding) je jiná technika, jak obrazit mnohorozměrná data do dvou či tří dimenzí.
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, random_state=0)
digits_tsne = pd.DataFrame(tsne.fit_transform(digits_df), columns=['TSNE1', 'TSNE2'])
plt.figure(figsize=(10,10))
sns.scatterplot(x=digits_tsne.TSNE1, y=digits_tsne.TSNE2,
hue=digits.target_names[digits.target], legend='full',
palette=sns.color_palette());
Filmová hodnocení
Všimněte si, že celou dnešní lekci jsme pracovali s daty, které byly na PCA jako dělaná. Co ale dělat, když budou data např. obsahovat chybějící hodnoty?
Problém si demonstrujeme na hodnocení 50 filmů 100 diváky, která jsou vybraná z databáze Movie Lens.
url_ratings = 'http://github.com/simecek/naucse.python.cz/blob/master/lessons/pydata/pca/static/ML_small.csv?raw=true'
ratings = pd.read_csv(url_ratings)
print(ratings.shape)
ratings.head()
scaler = StandardScaler()
ratings_scaled = scaler.fit_transform(ratings.drop(columns='title'))
Pravděpodobnostní PCA
Pravděpodobnostní (Probabilistic) PCA nám umožňuje doplnit chybějící pozorování. V Pythonu je implementovaná v knihovně PyPPCA.
# !pip install PyPPCA # odstraňte komentář pro instalaci balíčku
from pyppca import ppca
# značení podle ppca
C, ss, M, X, Ye = ppca(ratings_scaled, 2, False)
plt.figure(figsize=(15,15))
ax = sns.scatterplot(X[:,0], y=X[:,1])
for title, x, y in zip(ratings.title.values, X[:,0], X[:,1]):
ax.text(x, y, title, size='medium', color='black')
Hierarchické shlukování (clustering) a heatmapy
PCA graf není jediná metoda, jak zachytit souvislosti mezi jednotlivými pozorováními mnohorozměrných dat. Asi nejčastější alternativou je heatmapa doplněná dendrogramy hierarchického shlukování tak, jak ji můžete vidět na obrázku níže.
Povšimněte si, že podobně jako u PCA vidíme tři jasné shluky vzorků vín.
sns.clustermap(pd.DataFrame(wine_df_scaled, columns=wine_df.columns).T);
Shrnutí a závěrečné poznámky
V tomto notebooku jsme se naučili aplikovat na mnohorozměrná data Analýzu hlavních komponent (Principal Component Analysis, PCA) za účelem grafické reprezentace nebo snížení velikosti dat (pro zrychlení výpočtu či ušetření paměti).
Témata PCA příbuzná, která se sem už nevešla:
- Linear Discriminant Analysis technika příbuzná PCA, kde maximalizuje nikolik množství vysvětlené variability, ale množství informace vzhledem k jiné (závisle) proměnné
- Correspondence Analysis technika podobná PCA, ale aplikovaná na kategoriální, nikoli spojitá data
- Faktorová analýza: metoda používaná především v psychologii a psychometrii, matematický model jiný, ale též pomáhá odhalovat faktory za mnohorozměrnými daty
- Biplot PCA graf, kde krom pozorování jsou zanesené i vektory charakteristik (často používaný v R)
- Dvou nebo tří rozměrná PCA? U interaktivního grafu může být někdy dobrý nápad nakreslit 3-rozměrnou PCA. V opačném případě může 3-rozměrný graf "dobře vypadat", ale jinak pootočením ztrácíte informaci.
- Nespecifické filtrování charakteristik: pokud víte, že velká část vašich sloupců je konstantních, irelevantních apod. může být dobrý nápad je před PCA odfiltrovat (např. podle rozptylu)
- Pokud chcete vědět víc o PCA, přečtěte si příslušnou kapitolu z Data Science Handbook
- Zmínili jsme hierarchické clusterování (shlukování), ale už nám nezbyl čas na k-Means clustering
- A pokud byste potřebovali vysvětlit PCA svojí babičce, podívejte se na CrossValidated.
Domácí úkol
Vezměte si jednu z databází z předchozích hodin, například Pokémony nebo Gapminder (statistiky o jednotlivých státech) a pokuste se aplikovat, co jste se v této hodině naučili,
- ze numerických veličin nakreslete PCA graf
- spočítejte podíl variability vysvětlené prvními dvěma komponentami
- dají se PCA1 a PCA2 vysvětlit pomocí nějaké kategoriální proměnné
- zkuste PCA graf nakreslit jako interaktivní graf
- zkuste krom PCA grafu nakreslit i heatmapu s hierarchickým clusterováním
- pokuste se navrhnout, jak by šly do PCA zahrnout kategoriální veličiny, za předpokladu, že počet jejich kategorií není příliš velký (např. kontinent pro Gapminder nebo barva u pokémonů)