EDA - Analýza více proměnných a vztahů
V minulé lekci jsme se společně podívali na základy explorační datové analýzy a podrobněji jsme analyzovali proměnné každou zvlášť.
Následující lekce pokryje další část EDA - analýzu více proměnných současně a hledání vztahů mezi nimi.
Data k analýze jsou připravena v souboru salary.csv.
import pandas as pd
import seaborn as sns
%matplotlib inline
V dnešní lekci poprvé použijeme knihovnu seaborn. Seaborn je nadstavbou matplotlibu a přináší nám možnost vykreslit jeden velmi užitečný graf - tzv. heatmapu.
Načtení a kontrola dat
Nejprve si samozřejmě načteme data, která budeme dnes zpracovávat. Jedná se o informace o zaměstnancích, jejich věku, životním stylu, zkušenostech v oboru a platu. Našim cílem je zjistit, zda je mezi jednotlivými vlastnostmi zaměstnanců nějaký vztah.
Data, která dnes budeme analyzovat, jsou náhodně generovaná tak, aby alespoň některé ukázkové příklady hezky vycházely. Generování takových dat je samo o sobě náročný úkol.
data = pd.read_csv("static/salary.csv")
Načtení se zřejmě povedlo, ale jistotu získáme, až když si data prohlédneme.
Pro začátek uděláme klasickou sadu exploračních úkonů, abychom se s daty seznámili.
data
data.info()
data.isnull().sum()
data.describe()
data.hist(figsize=(20, 20));
Data se zdají být na první pohled v pořádku, neobsahují nulové hodnoty ani příliš mnoho odlehlých měření.
V datech máme následující informace:
- identifikační číslo zaměstnance ve sloupci id
- věk zaměstnance ve sloupci age (proměnná numerická, spojitá)
- míra aktivního životního stylu a zdravého stravování ve sloupcích active_lifestyle a healthy_eating - oboje označeno číslem od 0 do 10 (ordinální proměnné)
- počet měsíců v oboru ve sloupci months_of_exp (proměnná numerická, spojitá)
- měsíční mzda ve sloupci salary (proměnná numerická, spojitá)
Pro lepší představu o datech a také pro ukázku dalších technik a metod si do tabulky přidáme nový sloupec, který bude obsahovat měsíční mzdu v českých korunách.
data["salary_czk"] = data.salary * 23
data.describe()
Korelace a korelační koeficienty
Korelace znamená vzájemný vztah mezi dvěma veličinami nebo procesy. Ve statistice se tím nejčastěji myslí lineární vztah mezi dvěma proměnnými. Míra korelace se vyjadřuje korelačním koeficientem, který nabývá hodnot od -1 po 1.
- 1 znamená, že je mezi dvěma proměnnými přímá závislost a tedy když jedna proměnná roste, roste i druhá proměnná.
- 0 značí nulový vztah (absenci korelace).
- -1 znamená, že je mezi dvěma proměnnými nepřímá závislost a tedy když jedna proměnná roste, druhá proměnná klesá.
Korelační koeficient 1 nebo -1 nejčastěji znamená, že je jedna proměnná přímo vypočítaná z druhé a pro další analýzu většinou nemá žádný přínos. V praxi se korelační koeficienty těmto krajním hodnotám jen přibližují a naznačují tím, že stojí za to vztah mezi nimi prozkoumat hlouběji.
Korelace neimplikuje kauzalitu
Pozor na chybné závěry vyplývající z interpretace korelačních koeficientů. Korelace je nutnou, ale nikoli postačující podmínkou kauzality. Korelace znamená, že se dvě proměnné mění stejným způsobem, ale to nemusí znamenat, že nárůst jedné z nich zapříčiňuje nárůst druhé.
Příklad z Wikipedie:
- Korelace: Od 50. let 20. století prudce vzrostla jak úroveň atmosférického CO2, tak také výskyt obezity.
- Falešný závěr: Takže atmosférický CO2 způsobuje obezitu. (Nebo naopak obezita způsobuje nárůst CO2 v atmosféře.)
- Skutečná kauzalita: obojí je důsledkem toho, že bohatší populace víc jedí a zároveň spotřebovávají více energie.
Na webu spurious correlations je pak k nalezení celá řada podezřelých korelací, u nichž si kauzalitu lze představit jen těžko. Věděli jste například, že s klesajícím počtem svateb v Kentucky klesá i počet lidí, kteří se utopili po pádu z rybářské lodě? Náhoda? :)
Druhy korelací
Korelace lze identifikovat několika různými způsoby. Základní rozdělení je závislé na typu proměnných, které zkoumáme. Možné kombinace jsou:
- dvě numerické proměnné,
- dvě kategoriální proměnné nebo
- numerická a kategoriální proměnná.
První možnost je ta asi nejběžnější a proto je pro ni v pandasu vše připraveno a můžeme se rovnou podívat na všechny možné kombinace proměnných. K tomu nám poslouží scatter_matrix z modulu pandas.plotting.
Dvě numerické proměnné
from pandas.plotting import scatter_matrix
scatter_matrix(data, figsize=(20,20));
Scatter graf má na každé z os jednu proměnnou z datasetu a body označují jednotlivá individua odpovídající dané kombinaci hodnot. Jednotlivé body v grafu mohou mít také různou barvu či velikost, což umožňuje v jednom jednoduchém a dobře čitelném grafu zobrazit až 4 proměnné najednou a dělá to z něj velmi mocný nástroj.
Z jednotlivých grafů je tedy možné vyčíst, zda mezi proměnnými existuje korelace či nikoli. Někdy to v grafu však není tak úplně patrné a tak se určitě hodí i výpočet korelačního koeficientu.
Pokud nás nějaká kombinace proměnných v souhrnném grafu zaujme, můžeme si je snadno vykreslit jako samostatný graf pro danou kombinaci.
Kupříkladu závislost mezi mzdou a mzdou v korunách je naprosto jasně viditelná a také logická, protože jeden sloupec je vypočtený z druhého. Tady lze očekávat korelační koeficient na hodnotě 1. Vztah mezi mzdou a počtem měsíců v oboru je také dost dobře vidět, ale korelační koeficient z grafu tak snadno odhadnout nepůjde.
data.plot.scatter(x="salary", y="salary_czk");
data.plot.scatter(x="salary", y="months_of_exp");
Tabulku korelačních koeficientů získáme pomocí metody corr:
data.corr()
Tabulka korelačních koeficientů obsahuje na diagonále jedničky, protože každá proměnná je sama se sebou v dokonalé korelaci. Ve zbytku tabulky má smysl hledat hlavně hodnoty blízké krajním hodnotám korelačních koeficientů, k čemuž nám může dopomoci jednoduchá filtrace hodnot.
corr = data.corr()
corr[corr > 0.7]
Korelačním koeficientům proměnné healthy_eating se budeme věnovat později, protože se jedná o kategoriální proměnnou, která se nám v grafu a tabulce objevuje proto, že jsou její kategorie označeny číslem.
Dále je v tabulce jasně vidět vztah mezi mzdou a délkou zkušeností v oboru - obě proměnné rostou s korelačním koeficientem 0,799, což je vcelku vysoká hodnota.
Pearson vs Spearman
Pro výpočet korelace existuje více vzorců a tedy i více různých korelačních koeficientů. V tabulce výše máme Pearsonův korelační koeficient, který se hodí pro detekci lineárních vztahů, jak bylo vidět u přepočtené mzdy. Druhým častým koeficientem je Spearmanův, který se zase více hodí pro detekci monotónních vztahů.
Monotónní vztah si lze představit jako graf funkce, která v celém intervalu buď klesá nebo stoupá. Příklady jsou k dispozici na wikipedii.
Rozdíl si ukážeme na příkladu:
nums = range(1000)
values = [x**4 for x in range(1000)]
test = pd.DataFrame({"num": nums, "pow": values})
test
DataFrameje označení pro tabulku (lepší český ekvivalent asi neexistuje) a používá se i v jiných jazycích a statistických nástrojích. Doposud se nám DataFrame tvořil automaticky při načtení dat ze souboru, ale jak je vidět v tomto případě, je velmi snadné jej vytvořit i ručně a naplnit libovolnými daty. Když už jsme u pojmenování, jednotlivé sloupce naší tabulky jsouSeriea chovají se velmi podobně jako seznamy v Pythonu.
test.plot.line(x="num");
test.corr()
test.corr(method="spearman")
Pro vygenerovanou řadu čísel a jejich čtvrtou mocninu jsem nechal vypočítat oba korelační koeficienty. Oba byly vysoké, ale z rozdílu je vidět, že Pearsonův korelační koeficient zaregistroval, že vztah není lineární, zatímco Spearmanův odhalil dokonalou korelaci i v nelineárním vztahu.
V praxi se u nástrojů k tomu určených proto nejčastěji počítají oba koeficienty a ty už teď znáš rozdíl mezi nimi.
Dvě kategoriální proměnné
I když bychom v tomto případě mohli také využít scatter plot, zkusíme pro dvě kategoriální proměnné využít jiných, pro ně specifických metod, odhalování vzájemných vztahů.
Základním nástrojem je tzv. cross tabulka, která umí dle zadaných parametrů vypsat počet výskytů jednotlivých kombinací pro zkoumané kategorie. Pojďme se tedy podívat, zda existuje nějaká korelace mezi aktivním životním stylem a pohlavím zaměstnance:
pd.crosstab(data.sex, data.active_lifestyle)
Z tabulky je vidět, že zde nejsou žádné závratné rozdíly mezi muži a ženami v jednotlivých úrovních aktivního životního stylu. Pro grafickou reprezentaci stejné informace můžeme využít sloupcový graf, ve kterém necháme jednotlivé kategorie stát na sobě. Uvidíme tedy rozdíly mezi nimi a také rozdíl v celkovém počtu můžu a žen.
pd.crosstab(data.sex, data.active_lifestyle).plot.bar(stacked=True);
Když vytvoříme cross tabulku opačně (vyměníme řádky a sloupce), bude i její grafická reprezentace zobrazovat stejná data jiným způsobem.
pd.crosstab(data.active_lifestyle, data.sex).plot.bar(stacked=True);
pd.crosstab(data.active_lifestyle, data.sex).plot.bar(stacked=False);
Pojďme se podívat na kombinaci zdravého stravování a aktivního životního stylu.
crosstab = pd.crosstab(data.healthy_eating, data.active_lifestyle)
crosstab
V takto velké tabulce už není snadné vztah mezi dvěma proměnnými najít. Pro přesné statistické ověření (ne)závislosti kategoriálních proměnných se používají různé chi-square testy, jejichž podrobné vysvětlení je ovšem mimo rámec tohoto kurzu. Jejich problém je hlavně v tom, že jednotlivé proměnné musí splnit celou řadu kritérií, aby se dal test vůbec provést a podle některých kritérií se i volí správná varianta testu.
My si v tomto a následujících případech zkusíme vystačit s grafickou reprezentací. Tabulku si pomocí seabornu převedeme na tzv. heatmapu, která nám buňky obarví podle hodnoty.
crosstab = pd.crosstab(data.healthy_eating, data.active_lifestyle)
sns.heatmap(crosstab, annot=True);
Pokud by se v absolutních číslech dalo hůře vyznat, můžeme si nechat počet jednotlivých kombinací normalizovat (vydělit celkovým množstvím zaměstnanců) a to už je jen jedno násobení od procentuálního vyjádření.
crosstab = pd.crosstab(data.healthy_eating, data.active_lifestyle, normalize="all")*100
sns.heatmap(crosstab, annot=True);
Další užitečnou funkcí crosstab je možnost nechat si vypočítat součty pro jednotlivé řádky a sloupce.
pd.crosstab(data.healthy_eating, data.active_lifestyle, margins=True)
V tabulce je vidět, že nejvíce zaměstnanců je někde kolem průměru obou kategorií. To je dáno především distribucí dat, která je patrná z posledního řádku a sloupce.
Numerická a kategoriální proměnná
Zpět ke scatter plotu. Je-li možné kategoriální proměnnou vyjádřit číslem (healthy_eating nebo active_lifestyle), můžeme pro odhalování vztahů opět použít scatter plot.
Pojďme si ověřit něco, co bylo vidět v grafu od samotného začátku:
data.plot.scatter(x="salary", y="healthy_eating");
V grafu je vidět, že s rostoucím příjmem se zvyšuje i míra zdravého stravování. Vede zdravější stravování k lepším výsledkům a tedy vyšší mzdě? Nebo stojí vyšší mzda za utrácením více peněz za zdravé potraviny? To se z tohoto grafu nedozvíme, ale vztah tam očividně je a můžeme si jej i vyčíslit korelačním koeficientem (díky tomu, že kategorie jsou označeny číslem a vyšší číslo znamená lepší stravování).
data.corr()
K získání přesnějších informací o mzdách v jednotlivých kategoriích budeme potřebovat něco, čemu se říká seskupování. Seskupování probíhá tak, že se vybere jeden či více sloupců, které obsahují kategorie, které nás v tu danou chvíli zajímají. Celou tabulku podle těchto sloupců seskupíme (všechny řádky se stejnou kategorií slijeme dohromady) a řekneme pandasu, co má udělat se zbývajícími sloupci.
Pojďmě si celý proces ilustrovat na jednoduchém příkladu. Mějme jednoduchou tabulku se zaměstnanci:
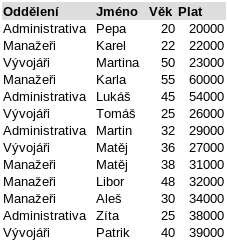
Po provedení operace groupby jsou řádky rozdělené do samostatných tabulek podle toho, který sloupec se pro seskupení použil. V tomto ilustračním příkladu jsme zaměstnance seskupili podle oddělení.
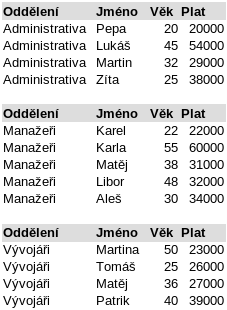
Posledním krokem je použití agregační funkce, která spojí tabulky zpět dohromady tak, že každou z nich nejdříve agreguje do jednoho řádku. V našem případě se vypočte průměr, což mimo jiné znamená, že přijdeme o sloupce, ze kterých průměr vypočíst nelze.

Zpět k našim datům. Jak asi vypadá průměrná mzda pro jednotlivé míry zdravého stravování?
data.groupby("healthy_eating").mean()
Při takovém seskupení se ze sloupce healthy_eating stal index a ze všech ostatních numerických sloupců se pro jednotlivé kategorie vypočetl průměr. Stejně jako v ilustračním příkladu.
Kromě průměru existují i agregační funkce pro sumu, počet záznamů, minimum, maximum a další deskriptivní statistiky.
Pojďme si výsledek ukázat v grafu a zjistit, zda potvrdí naši hypotézu.
data.groupby("healthy_eating").mean().plot.bar(y="salary");
Je to skutečně tak. S rostoucí mzdou se zvyšuje i pravděpodobnost, že zaměstnanec se bude zdravěji stravovat. V grafu ale máme průměrné mzdy, což může znamenat, že některé sloupce ovlivňují odlehlá měření. To by mohlo znamenat, že vysokou mzdu u velmi nezdravého stravování způsobuje jen několik jedinců se zálibou ve fastfoodech. Ověřit si toto tvrzení můžeme známým boxplotem, který nám prozradí, kolik odlehlých měření v jednotlivých sloupcích máme. Všimněte si, že boxplot umí seskupování udělat úplně sám a není mu tak třeba data připravovat předem.
data.boxplot(column="salary", by="healthy_eating");
Ukázalo se, že náš předpoklad byl mylný. Vztah mezi mzdou a mírou zdravého stravování není zcela lineární a odlehlá pozorování na to nemají vliv.
Pojďme se podívat ještě na jeden vztah, který z úvodní matice scatter plotů nebyl tak úplně zřejmý a korelační koeficient pro něj nebyl vysoký - závislost mzdy na aktivním životním stylu. Nejprve v obyčejném grafu s průměry pomoci groupby:
data.groupby("active_lifestyle").mean().plot.bar(y="salary");
I když průměrná mzda zaměstnance klesá, čím aktivnější jeho životní styl je, oba korelační koeficienty vyšly velmi blízko nule. Čím to? K řešení nás přivede boxplot:
data.boxplot(column="salary", by="active_lifestyle");
Jak je v boxplotu vidět, ve všech kategoriích aktivního životního stylu je celkem velký rozptyl možných platů a tak z klesajícího průměru není možné vyvozovat silné závěry.
Pro tuto kombinaci proměnných také existují statistické testy jako např. ANOVA, T-test, Z-test atp. Jejich výběr je ale ještě složitější než u předchozí kombinace dvou kategoriálních proměnných.
Na co si dát pozor
Korelace a křivky
Při prvním pokusu o zkoumání vztahů na začátku lekce jsme se nedívali na graf jen tak pro nic za nic. Existují totiž situace, kdy je v grafu vztah dvou proměnných zřejmý, ale korelační koeficienty o tom nevypovídají. Příkladem mohou být křivky, u kterých je vztah viditelný, ale špatně se detekuje početně.
from random import randrange
nums = []
values = []
for x in range(-10, 11):
for _ in range(10):
nums.append(x)
values.append(randrange(x**2-10, x**2+10))
test = pd.DataFrame({"num": nums, "value": values})
test
Jako základní tvar nám posloužila kvadratická funkce a pro každé číslo na ose X jsme vygenerovali deset náhodných čísel okolo paraboly.
Z grafu je vztah mezi těmito proměnnými jasně patrný:
test.plot.scatter(x="num", y="value");
Ovšem korelační koeficienty jej nechají bez povšimnutí:
test.corr()
test.corr(method="spearman")
Korelace a odlehlá pozorování
Nejen tvar grafu znázorňující vztah mezi proměnnými, ale i odlehlá měření mohou mít velmi negativní vliv na výsledky korelačních koeficientů.
nums = []
values = []
for x in range(20):
for _ in range(3):
nums.append(x)
values.append(randrange(x*2-3, x*2+3))
test = pd.DataFrame({"num": nums, "value": values})
test.plot.scatter(x="num", y="value");
test.corr()
Opět máme náhodně generovaná data tentokrát s drobným rozptylem kolem přímky. A korelační koeficient je dle očekávání velmi vysoký. Pojďme se podívat, co se stane, když do našich dat přidáme pár odlehlých měření.
test.loc[60] = 20, 0
test.loc[61] = 21, 0
test.loc[62] = 22, 0
test.plot.scatter(x="num", y="value");
test.corr()
Jak je vidět, stačí jen pár odlehlých měření, která jsou navíc zcela očividně mimo očekávání, a korelační koeficient na to ihned reaguje rapidním poklesem.
V jedné z následujících lekcí se naučíme, jak odlehlá měření správně detekovat a jak se s nimi vypořádat.
Čas na hraní
Stejně jako po minulé lekci i tentokrát budeš mít fůru času zkusit si nově získané vědomosti a schopnosti aplikovat na svých datech. Po minulé lekci znáš vybraná data a jednotlivé proměnné v nich jako své boty a tak jistě nebude problém na ně aplikovat novinky z této lekce.