EDA - Reprezentativnost dat a centrální limitní věta
Z minulých lekcí už známe základní metody datové analýzy a umíme aplikovat obecné postupy a komplexní nástroje tak, abychom z dat dostali zajímavé informace.
Situaci nám v tomto snažení mohou komplikovat chybějící data a různé další chyby vedoucí k odlehlým měřením, které se dají s trochou štěstí detekovat a je možné se s nimi nějak vypořádat. Co když ale data vypadají naprosto perfektně, ale výsledky, i přes precizně provedené statistické výpočty, budou úplně k ničemu? Jak se tohle vůbec může stát?
Dnes se společně podíváme na to, jak důležitou roli v našem snažení hrají data samotná a správný způsob jejich sběru, jak se dají podvrhnout výsledky analýzy ještě před tím, než se o ní někdo vůbec pokusí, a jak využít centrálně limitní větu k tomu, abychom se toho vyvarovali.
Špatná data nikdy neposkytnou dobré výsledky
U dat platí známé Garbage in - garbage out, a tedy, i kdyby naše výpočty a analytické nástroje byly naprosto precizní a bez chyby, pokud do nich nasypeme odpad na vstupu, nic jiného než odpad na druhé straně nemůžeme očekávat.
Reprezentativnost dat
Problém spočívá hlavně v tom, že většinu času potřebujeme pracovat se vzorky z celkového množství dat, protože nejsme schopni získat celková data od všech.
Pokud budu chtít analyzovat vývoj spotřeby elektřiny u sebe doma a budu pravidelně po dobu několika let odečítat hodnoty z elektroměru, budu mít veškerá potřebná data k dispozici. Pro zjištění vlivu na vývoj spotřeby je pak mohu zkusit spojit s informacemi o počasí či s významnými událostmi v kalendáři. V tuto chvíli mám k dispozici vše potřebné.
Co když mě ale bude zajímat názor Poláků na potraty? Není v silách nikoho zeptat se každého jednotlivého Poláka na jeho názor a sesbíraná data pak analyzovat jako kompletní datovou sadu. V takovém případě si budu muset vystačit s dobře vybraným (tzv. reprezentativním) vzorkem populace Polska. Jenže jak jej vybrat? Náhodně!
Pojem populace je obecný a označuje všechna data, která existují. Pokud pro svůj výzkum nemáme přístup k celé populaci, potřebujeme získat reprezentativní vzorek (sample). Při analýze spotřeby elektřiny u mě doma, analýze účetnictví mého zaměstnavatele nebo prospěchu svých dětí mám k dispozici celou populaci. U analýzy názorů Evropanů se budu muset spokojit se vzorkem populace. Pak je tu ještě střední cesta. Například při analýze filmů si nemohu být jist, zda je mám v datasetu staženém z internetu úplně všechny, ale vzorek, který mám k dispozici, je tak velký, že jej pro potřeby konkrétní analýzy mohu považovat za populaci a jeho reprezentativností se netřeba trápit.
Abychom byli schopni odhadnout názor polské populace na potraty, potřebujeme vytvořit dobrý reprezentativní výběr, což je daleko těžší, než se zdá. Základem je vybrat z obyvatel dostatečné množství jedinců a hlavně je v ideálním případě vybírat zcela náhodně. Zatímco získání dostatku odpovědí je s dostatkem peněz a času celkem snadné, náhodný výběr je velmi komplexní disciplína. Tak například:
- Když udělám dotazníkové šetření před budovou nádraží, budu tam mít respondenty, kteří z jakéhokoli důvodu preferují hromadnou dopravu nebo prostě nemají na auto peníze. Tímto úplně ignorujeme lidi jezdící autem nebo ty pracující z domu. A navíc, řada introvertních lidí vás obejde obloukem a nebude ochotna odpovídat na otázky.
- Pokud jen vystavím dotazník na internetu, vyplní mi jej jen respondenti, kteří na to mají čas a jsou v tomto směru aktivnější. Existují i platformy, kde za vyplnění dostávají respondenti zaplaceno. Tam se ale může snadno stát, že ve snaze vyplnit co nejvíce dotazníku v co nejkratším čase budou odpovědi náhodné, protože si respondent ani nepřečte otázku.
- Telefonická šetření také získají odpovědi od respondentů, kteří mají čas a chuť si s operátorem povídat a neblokují tato telefonní čísla.
Pokud získáme data jakýmkoli z těchto způsobů, nebudou výsledky analýz ani v nejmenším reprezentativní, protože při získávání respondentů jsme ignorovali značnou část populace. Tomuhle se říká selektivní zkreslení (selection bias).
Situace je ještě komplikovanější, pokud děláte výzkum vlivu nějakého faktoru (třeba konkrétního léku). V takovém případě potřebujeme dvě skupiny respondentů, které se liší jen v tom, zda lék užívají či nikoli, ale všechny ostatní faktory jsou zcela náhodné. To je velmi problematické. Pokud je například lék drahý, je velmi pravděpodobné, že ve skupině jeho uživatelů budou lidé s vyšším příjmem. Bohatší lidé si mohou dovolit kvalitnější a zdravější jídlo a předplatné v posilovně, a tak za jejich uzdravením vůbec nemusí být lék samotný, ale spousta dalších faktorů, které se u druhé skupiny neobjevují a jejichž vliv se nepodařilo snahou o náhodný výběr odstranit.
Dobře vybraný náhodný vzorek je jako polévka. Pokud ji pořádně nezamícháte, budete na začátku jist jen vodu bez chuti a na konci příliš intenzivní směs zeleniny, nudlí a koření.
Data mohou být ovšem zkreslena (tzv. bias) mnoha dalšími způsoby:
- Výše popsaný problém s nenáhodným výběrem (selection or self-selection bias)
- Zkreslení pamětí (recall bias) - lidé mají od přírody selektivní paměť a čím vzdálenější je oblast, na kterou se ptáme, tím více zkreslené mohou být výsledky. Například lidé trpící nějakou nemocí si budou zdánlivě lépe pamatovat rizikové faktory z minulosti, protože sami sobě budou chtít zdůvodnit, proč tu či onu nemoc mají. Kdyby o své diagnóze nevěděli, jejich odpovědi by mohly lépe vystihovat realitu.
- Zkreslení pozorovatelem (observer bias) - osoba dělající výzkum se ptá způsobem, který záměrně ovlivní odpovědi nebo v datech automaticky hledá to, co v nich očekává.
- Zkreslení přeživších (survivorship bias) - Zaměření se jen na respondenty, kteří už prošli nějakým výběrem, což může limitovat jejich náhodnost. Například analyzované průměrné výsledky studentů střední školy jsou s každým rokem lepší a lepší, protože ti nejhorší studenti školu postupně opouštějí.
Rozdělení pravděpodobnosti
Nelekej se! Nepopulární látku z hodin statistiky si přiblížíme prakticky a jednoduše.
Představ si nějakou proměnnou - třeba hmotnost člověka. Rozdělení pravděpodobnosti, které tato proměnná má, nám říká, jak pravděpodobné je, že potkáš člověka s nějakou konkrétní hmotností. Asi intuitivně tušíme, že potkat člověka se 75 kg je daleko snazší a děje se to častěji než setkání s člověkem, který má 200 kg. A tuhle intuici nám rozdělení pravděpodobnosti jen převádí na konkrétní čísla.
Rovnoměrné rozdělení
Rovnoměrné rozdělení je takové, kde mají všechny možnosti stejnou šanci nastat. Je to asi nejjednodušší rozdělení pravděpodobnosti, protože si jej lze představit jako hody (poctivou) kostkou nebo mincí. U hodu kostkou máme šest možností, které mohou nastat se stejnou pravděpodobností. U mince jsou jen dvě.
Graf šedesáti hodů kostkou bude v ideálním případě vypadat následovně:
Normální rozdělení
Daleko zajímavější než rovnoměrné rozdělení je normální rozdělení. O normálním rozdělení už byla řeč v jedné z minulých lekcí. Hlavní charakteristika normálního rozdělení spočívá v tom, že nejčastěji se v populaci vyskytuje nějaká průměrná hodnota a čím více se od průměru vzdálíme, tím menší je pravděpodobnost, že se s takovou hodnotou setkáme. Vzpomínáte na graf výšky a hmotnosti u mužů a žen? Graf tvaru zvonu je pro normální rozložení typický.
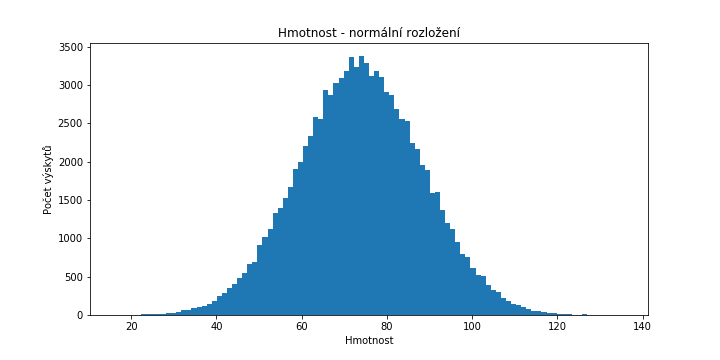
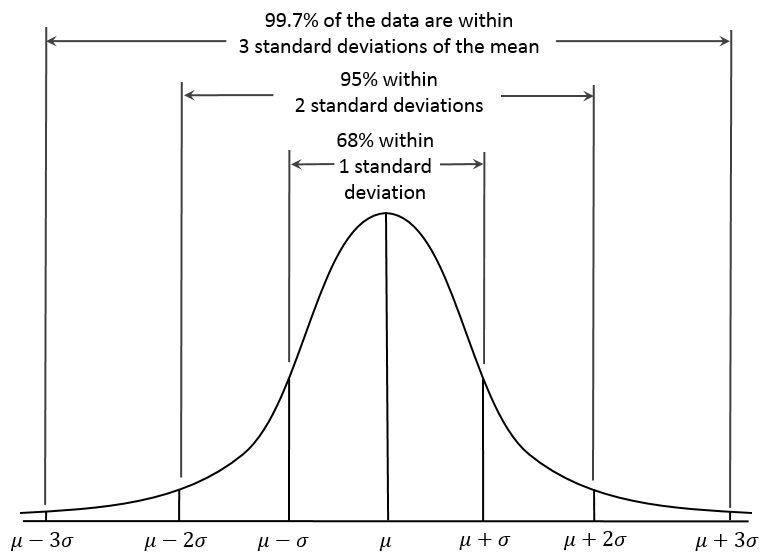
Další zajímavostí normálního rozdělení je, že se s ním potkáme u spousty proměnných, se kterými budeme v analýzách pracovat - výsledky testů, rozdělení příjmů, výška, hmotnost, atp. Díky jeho častému výskytu v běžném životě je i spousta algoritmů strojového učení přizpůsobena k nejlepšímu fungování právě s proměnnými s normálním rozdělením. Pokud u nějaké proměnné normální rozdělení pravděpodobnosti detekujeme (nejčastěji prostým pohledem na histogram), má hned k dispozici jedno velmi užitečné pravidlo týkající se procentuálního pokrytí populace v závislosti na vzdálenosti od průměru v násobcích směrodatné odchylky.
zdroj: Wikipedia
Exponenciální rozdělení
Příkladem z jiného soudku může být exponenciální rozdělení pravděpodobnosti, jehož graf (histogram) má tvar exponenciální funkce.
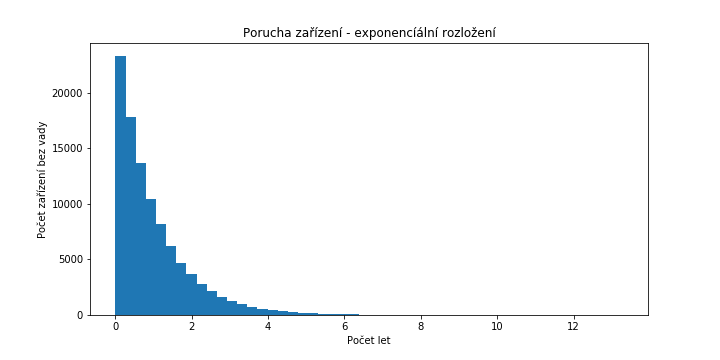
Praktickým příkladem proměnné s takovým rozložením může být např. doba, za jakou se pokazí nějaký spotřebič. Budeme-li uvažovat, že v každém okamžiku je pravděpodobnost objevení se poruchy konstantní (což je idealizovaná aproximace, přibližně platná pro některé druhy výrobků), bude exponenciálně klesat pravděpodobnost, že máme doma funkční kus - nejdříve rychle, pak stále pomaleji, až se nakonec bude asymptoticky blížit nule.
Další rozdělení
Rozdělení pravděpodobnosti je daleko více a často se liší jen v detailech. Vybrat to správné a ověřit, že daná proměnná je skutečně distribuována tímto způsobem, může být důležité pro některé konkrétní statistické výpočty. Následující schéma ukazuje celou řadu různých rozdělení a vztahů mezi nimi:
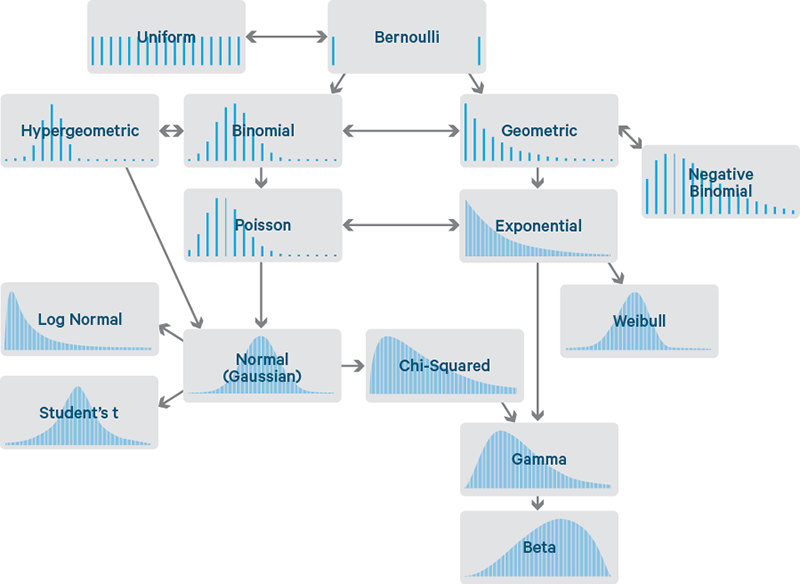zdroj: towardsdatascience.com
K čemu je to dobré?
Mimo již napsaného nám znalost rozložení pravděpodobnosti může pomoci zodpovědět užitečné otázky. Když se například podíváme na graf normálního rozložení platů učitelů, můžeme si odpovědět na otázku, jak je pravděpodobné, že učitel vydělává více, než je určitá hodnota. Ke každému rozložení pak existují vzorce, které nám pomohou se ke konkrétní hodnotě pravděpodobnosti dopočítat.
Centrální limitní věta (Central limit theorem)
Jak souvisí rozdělení pravděpodobnosti s reprezentativností dat? Velmi. A znalost centrální limitní věty (CLT) nám to pomůže dokázat.
CLT nám říká, že pokud budeme z proměnné s libovolným rozdělením pravděpodobnosti vytvářet vzorky, budou průměry (ale i jiné popisné statistiky) těchto vzorků mít normální rozdělení. A čím početnější tyto vzorky budou, tím blíže ideálu bude i normální rozdělení z nich vytvořené.
Tohle si říká o příklad. Mějme populaci složenou z miliónu hodů klasickou kostkou.
import pandas as pd
import numpy as np
%matplotlib inline
hody = np.random.randint(1, 7, 1000000)
Milión náhodných čísel v intervalu <1, 7) si převedeme na DataFrame a koukneme na histogram a základní popisné statistiky.
populace = pd.DataFrame(hody, columns=["hody"])
populace.hist(bins=11);
populace.describe()
populace.hody.value_counts()
Běžná hrací kostka zaručuje, že se při miliónu pokusů objeví každá hodnota v přibližně stejném počtu. Tato proměnná má tedy rovnoměrné (uniformní) rozložení pravděpodobnosti.
Co se stane, když si z takovéto populace začneme vybírat vzorky? Pro názornost začneme s velmi malými vzorky o velikosti 3 a pro každý takový vzorek vypočítáme průměr a uložíme jej do nového seznamu.
prumery_hodu = []
for _ in range(1000):
prumery_hodu.append(populace.sample(n=3).hody.mean())
Seznam si opět převedeme na DataFrame a podíváme se, co nám z průměrných hodnot tisíce samostatných vzorků vzniklo.
prumery_hodu = pd.DataFrame(prumery_hodu, columns=["prumery_hodu"])
prumery_hodu.plot.hist(bins=15);
prumery_hodu.describe()
Z průměrů naších vzorků nám vzniklo téměř ideální normální rozložení. Průměrem všech průměrů jsme se také dostali velmi blízko průměru celé populace. Problém je, že v histogramu je vidět i nezanedbatelný počet extrémních hodnot na obou stranách grafu, kdy jsme při náhodném výběru obdrželi vzorky s třemi jedničkami či třemi šestkami. Jak je vidět, příliš malé vzorky jsou velmi náchylné k výskytu odlehlých měření (méně pravděpodobných kombinací hodnot ve vzorku) a nemusí být ve výsledku reprezentativní.
Pojďme zkusit ještě jednou stejný pokus, ale tentokrát udělat každý vzorek desetkrát větší.
prumery_hodu = []
for _ in range(1000):
prumery_hodu.append(populace.sample(n=30).hody.mean())
prumery_hodu = pd.DataFrame(prumery_hodu, columns=["prumery_hodu"])
prumery_hodu.plot.hist(bins=15);
prumery_hodu.describe()
Graf opět vypadá jako graf normálního rozložení, ale tentokrát je užší a neobsahuje extrémní hodnoty ani na jedné straně. Směrodatná odchylka je tím pádem podstatně menší. Z toho všeho vyplývá, že podstatně větší množství z tisíce vybraných vzorků bylo blíže průměru a mělo i ostatní popisné statistiky podobné jako celá populace.
Díky vlastnostem normálního rozložení můžeme také prohlásit, že přibližně 68 % našich vzorků z druhého pokusu je v rozmezí mean ± std = (3,186; 3,802) a přibližně 95 % našich vzorků je v rozmezí mean ± 2×std tedy (2,878; 4,11). Přibližně proto, že získané rozložení nemá ideální "normální" tvar. A při výběru konečného množství vzorků (navíc z konečné populace) ani mít nemůže.
Jaká je tedy ta správná velikost vzorku?
Odpověď na tuhle otázku není jednoduchá. Více je samozřejmě lépe, jak jsme si dokázali s použitím CLT, ale limitujícím faktorem jsou často peníze a čas. Velké společnosti zaměřené na výzkumy veřejného mínění mají dostatek obojího a tak je lepší to nechat na nich. Nicméně i tak existuje pár pravidel, kterými je možné se řídit.
Minimum je 100
Se vzorkem velikosti 100 se už dají dělat různé pokusy a výpočty a je možné od nich očekávat alespoň nějaké užitečné odpovědi. Pokud je populace menší než 100, je potřeba ji prozkoumat celou.
Maximum je 10 % nebo 1000
Pokud má populace 5000 individuí, mělo by nám stačit získat informace o pěti stovkách z nich. Nemusíme při tom ale překročit tisícovku, takže pro populaci o 200 000 individuích i 10 000 000 by nám měl postačit stejně velký vzorek. Je ale třeba mít na paměti náhodnost výběru.
Zbývá vybrat něco mezi
V závislosti na:
- množství času a peněz,
- nutnosti získat opravdu přesné výsledky,
- potřebě rozdělit individua ze vzorku na menší skupiny dle nějakého kritéria,
- předpokladu, že respondenti budou dávat podobné odpovědi,
- či důležitosti a dopadech rozhodnutí, které z takového výzkumu nakonec vyvstane.
Každý chce mít co nejpřesnější výsledky, takže limitujícím faktorem jsou často peníze a čas a dokud jedno nebo druhé nedojde, výzkum pokračuje dále.
Podpořeno čísly
Existuje několik vzorců, které umožní podpořit ten správný výběr velikosti vzorku vypočteným číslem. Výběr toho správného není snadný a závisí na našich znalostech populace. Jeden z jednodušších vzorců, pro jehož výpočet nám stačí znát velikost populace, je Yamane (podle jména svého autora). Vypadá takto:
$$ n = \frac{N}{(1+Ne^2)} $$
n je výsledná velikost vzorku, N značí celkovou velikost populace a e je označení pro přípustnou chybu. Přípustná chyba je obrácenou hodnotou úrovně spolehlivosti výběrů. Pokud budeme například požadovat, aby nás výzkum vyšel stejně v 97 % případů, bude
$$ e = \frac{100 - 97}{100} = 0.03 $$
Pro lepší představu by se výsledky takových výpočtů daly shrnout do jednoduché tabulky, která poslouží, pokud by jednoduchá pravidla z předchozích odstavců nebyla dostatečná.
| Velikost populace | |||||
| Přípustná chyba | 5000 | 2500 | 1000 | 500 | 200 |
| ±10 % | 98 | 96 | 91 | 83 | 67 |
| ±7,5 % | 172 | 166 | 151 | 131 | 94 |
| ±5 % | 370 | 345 | 286 | 222 | 133 |
| ±3 % | 909 | 769 | 526 | 345 | 169 |
Čas na hraní (a přemýšlení)
Tato lekce je spíše teoretická, ale rozhodně přináší hodně podnětů k zamyšlení. Můžeš opět vzít svou datovou sadu a předchozí analýzy a zamyslet se nad následujícími otázkami:
- Pracuješ se vzorkem nebo s celou populací? Dá se to nějak ověřit?
- Je vzorek reprezentativní?
- Jak složité by bylo získat data celé populace nebo si vytvořit vlastní reprezentativní vzorek?
- Kolik peněz by stálo položit nějakou zajímavou otázku reprezentativnímu vzorku české populace?
- Jaké rozložení mají proměnné ve tvých datech? Je tam nějaká, na kterou žádné rozložení pravděpodobnosti nepasuje?