Klasifikační metriky
Úloha klasifikace je trochu jiná než úloha regrese, proto má své vlastní metody na posuzování úspěšnosti modelů. Projdeme nejdůležitější metriky určené pro klasifikaci.
Abychom mohli metriky rovnou ilustrovat na příkladu, vezměme si na pomoc známou datovou množinu Iris. Jedná se o klasifikaci květů (amerických) kosatců. Datovou množinu ve třicátých letech sestavil statistik a biolog Ronald Fisher (viz wiki). Množina obsahuje tři třídy: setosa, versicolor a virginica.
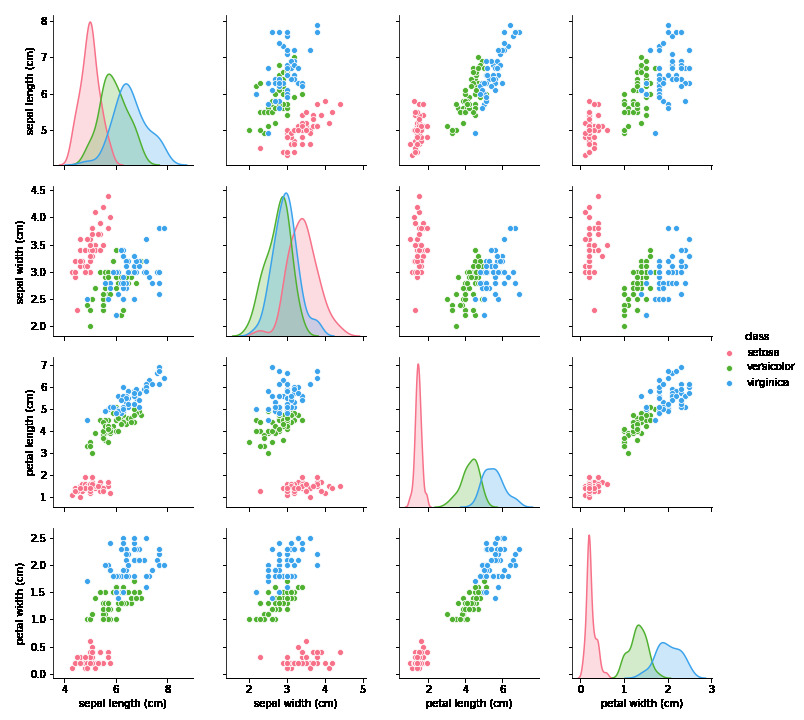
Na obrázku vidíte pairplot zobrazující závislosti mezi dvojicemi příznaků (vstupními proměnnými) a výslednou třídou. Barva tečky odpovídá třídě, do které daný kosatec patří. Vidíte např. že červená třída setosa se dá určit dle velkosti okvětního (petal lístku).
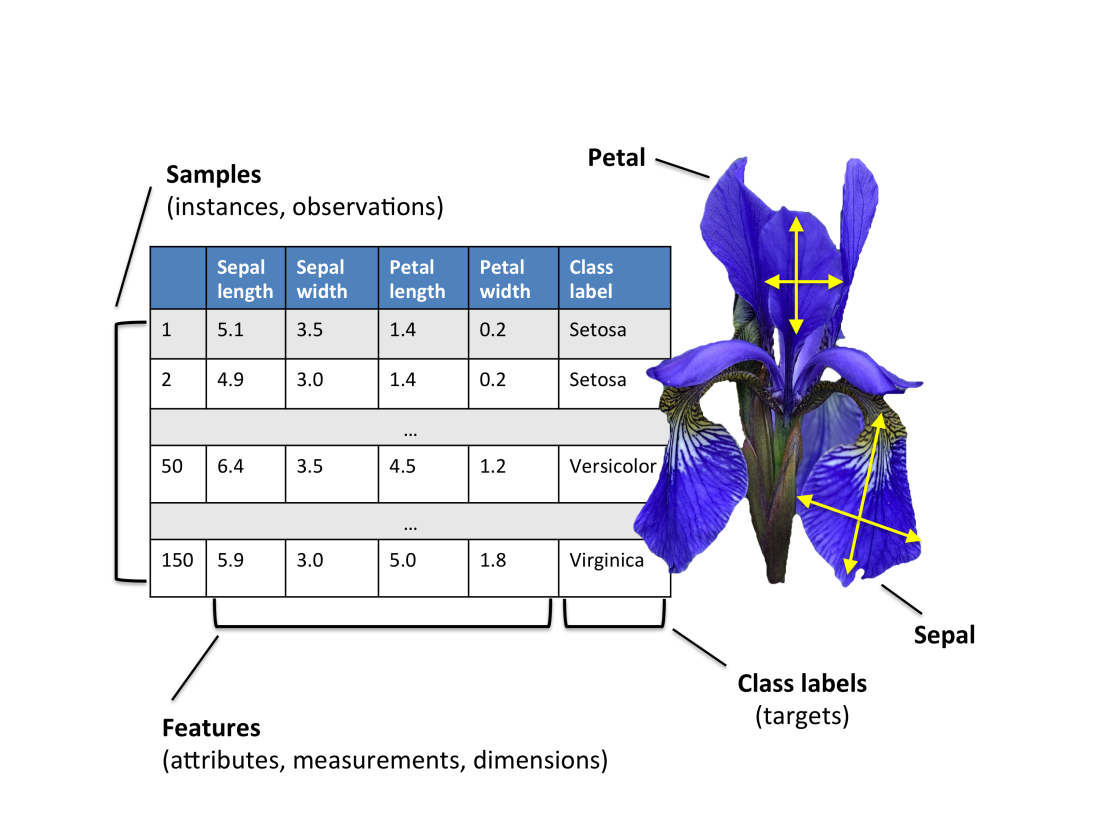
Cílem úlohy je vytvořit model -- klasifikátor, který nám pro dané hodnoty kališních (sepal) a okvětních (petal) lístků vrátí správné zařazení daného vzorku do třídy.
Jako klasifikátor zvolme rozhodovací strom, t. j. DecisionTreeClassifier. (Je to jeden z nejznámějších klasifikátorů, oblíbený zejména díky své rychlosti a snadné interpretovatelnosti. Více si o něm můžeš přečíst na wiki).
Nás tedy bude zajímat, jak můžeme měřit úspěšnost našeho klasifikátoru.
(Data tentokrát nečteme ze souboru, ale použijeme předpřipravená data z modulu datasets knihovny Scikit-learn).
# tohle tu máme jen proto, aby všechny výpočty proběhly stejně
# nastavení náhodného generátoru
import numpy as np
np.random.seed(42)
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
iris = datasets.load_iris() # načteme si data, Iris data jsou "vestavěná"
X = iris.data # příznaky
y = iris.target # třídy (labely)
# rozdělme data na trénovací a testovací
# random_state určuje inicializaci generátoru náhodných čísel (chceme aby nám to vždy vyšlo stejně)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2, random_state=314)
# vytvořme klasifikátor
klasifikator = DecisionTreeClassifier(random_state=314)
# natrénujeme a ohodnotíme testovací množinu
klasifikator.fit(X_train,y_train)
y_pred = klasifikator.predict(X_test)
Podívejme se, jak predikce vypadají.
print(f"{'Příznaky:':^25} {'Predikovaná třída:':^25} {'Skutečná třída:':^25}")
print("_" * 92)
for priznaky, trida_pred, trida_skut in zip(X_test, y_pred, y_test):
result_str = "OK" if trida_pred == trida_skut else ":("
print(f"{str(priznaky):^25} {trida_pred:^25} {trida_skut:^25} {result_str:^25}")
Nejjednodušší, co můžeme měřit, je procento správných odpovědí. Tomu se říká accuracy.
100 * ((y_pred == y_test).sum() / len(y_test))
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_pred)
Úkol:
Představ si, že máš klasifikovat jablka a hrušky. Máš datovou množinu obsahující 100 kusů ovoce. Klasifikátor na této množině dosahuje úspěšnosti 90% (90 kusů je klasifikováno správně). Myslíš, že takový klasifikátor je dobrý?
Accuracy nám dává velmi málo informace. Prozradíme si nyní, že v úkolu s ovocem bylo 90 kusů jablek a 10 kusů hrušek. Klasifikátor, který vše, co dostane, označuje za jablko, má tedy na této množině 90% úspěšnost. Nám je ale k ničemu.
from sklearn.metrics import plot_confusion_matrix
import matplotlib.pyplot as plt
%matplotlib inline
plot_confusion_matrix(klasifikator, # naučený klasifikátor
X_test, y_test, # data
display_labels=iris.target_names, # jména tříd [lze vynechat]
cmap=plt.cm.Blues # barevná paleta [lze vynechat]
);
Matice záměn (confusion matrix) nám dává daleko více informace. Na obrázku vidím, kolik vzorků z třídy dané řádkem bylo klasifikováno do třídy dané sloupcem.
Tedy v našem případě: Jeden vzor typu Virginica byl oklasifikován chybně jako Versicolor, dva vzory typu Versicolor byly oklasifikovány chybně jako Virginica.
Nyní se podíváme na binární klasifikaci (klasifikaci do dvou tříd). Vezměme si data breast_cancer, která obsahují pozitivní a negativní rakovinové nálezy. Abychom měli srovnání různých řešení, vezmeme si dva klasifikátory, jednak SVC (Support Vector Machine klasifikátor, česky metoda podpůrných vektorů, ale český název se nepoužívá. Více informací viz wiki) a druhak tzv. Dummy klasifikátor, který slouží pouze jako baseline a implementuje triviální řešení.
from sklearn.svm import SVC
from sklearn.dummy import DummyClassifier
# natáhneme data a rozdělíme na trénovací a testovací
X, y = datasets.load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# vytvoříme a natrénujeme klasifikátory
klasifikator = SVC(random_state=0, probability=True)
klasifikator.fit(X_train, y_train)
dummy = DummyClassifier()
dummy.fit(X_train, y_train)
# oklasifikujeme si testovací vzorky
y_pred = klasifikator.predict(X_test)
y_dummy = dummy.predict(X_test)
# spočteme accuracy
print("SVC accuracy ", accuracy_score(y_test, y_pred))
print("dummy accuracy ", accuracy_score(y_test, y_dummy))
plot_confusion_matrix(klasifikator, X_test, y_test, cmap=plt.cm.Blues);
Třídu 0 označujeme jako negativní, třídu 1 jako positivní. Jeden pozitivní vzorek byl označen za negativní, takovýmto případům říkáme falešně negativní (false negative). Osm negativních vzorků bylo označeno jako positivní, to jsou tzv. falešně positivní (false positive) vzory.
Počty falešně positivních a falešně negativních případů jsou pro hodnocení úspěšnosti binární klasifikace zásadní. Správně klasifikované vzorky označujeme jako true positive a true negative.
Obrázek ilustruje rozdělní vzorků na true positive, true negative, false negative a false positive. Zelená barva reprezentuje pozitivní vzorky, červená negativní. Vzorky uvnitř kola označil klasifikátor jak pozitivní (zelené jsou tedy true positive a červené false positve. Vzorky vně kola, označil klasifikátor jako negativní, ty zelené jsou tedy false negative a červené true negative.

Precision, recall, F1 skóre
Klasifikační metrika známá jako precision říká, kolik vzorků označených za pozitivních je opravdu pozitivních.
$$ precision = \frac{TP}{TP+FP} $$
TP označuje počet správně označených pozitivních vzorků (true positives)
FP označuje počet falešně pozitivních vzorků (false negatives)
Metrika recall říká, kolik pozitivních vzorků bylo podchyceno klasifikátorem (klasifikováno jako pozitivní).
$$ recall = \frac{TP}{TP+FN} $$
FN je počet falešně negativních vzorků (false negatives)
Nesnaž se vzorečky zapamatovat, zamysli se nad tím, co nám říkají. S tím ti pomůže obrázek výše a následujíc příklad z Wikipedie.
Představ si, že máš počítačový program na rozpoznávání psů na fotografiích. Máš fotku 12 psů a několika koček. Program ti na fotografii najde 8 psů. Pět z těchto 8 psů jsou opravdu psi (true positive), ale zbylí dva jsou ve skutečnosti kočky (false positive). Precision programu je 5/8 (0.625), zatímco recall je 5/12 (cca 0.417). Precision se dá interpretovat jako míra užitečnosti výsledku, recall říká, jak moc je výsledek kompletní (kolik psů z těch co jsme chtěli najít, jsme opravdu našli).
from sklearn.metrics import precision_score, recall_score
print("Precision: ", precision_score(y_test, y_pred))
print("Recall: ", recall_score(y_test, y_pred))
print("Precision: ", precision_score(y_test, y_dummy))
print("Recall: ", recall_score(y_test, y_dummy))
Zda je pro nás důležitější precision nebo recall, záleží na konkrétní úloze. Někdy vadí více falešně pozitivní případy (příliš mnoho relevantních mailů označených za spam), jindy bude více vadit nezachycený pozitivní případ (neodhalený výskyt nemoci).
Další často používanou metrikou je tzv. F1 skóre. Kombinuje precision a recall, a to tak, že obě tyto metriky mají stejnou váhu (Přizpívají stejnou měrou k výsledku). Čím větší hodnota, tím lepší výsledek. Maximální hodnota je jedna, minimální 0.
$$ F1 = 2 \frac{precision \cdot recall}{precision + recall}$$
from sklearn.metrics import f1_score
print("F1 skóre SVC: ", f1_score(y_test, y_pred))
print("F1 skṕre Dummy: ", f1_score(y_test, y_dummy))
ROC křivka
Další užitečná charakteristika je tzv. ROC křivka (wiki). Název pochází z anglického Receiver Operating Characteristic, operační charakteristika přijímače. Křivka vyjadřuje kvalitu binárního klasifikátoru v závislosti na klasifikačním prahu.
Co je to klasifikační práh? Představ si, že v úloze na breast cancer nebude naučený model vracet hodnoty 0/1 (negativní, pozitivní nález), ale číslo typu float udávající pravděpodobnost (nebo nějakou míru) náležení do pozitivní třídy.
V nejjednodušším případě budeš vzorky s pravděpodobností větší než 0.5 klasifikovat jako pozitivní, ostatní jako negativní. Můžeš ale chtít být opatrná a dovyšetřit i pacienty, kteří mají horší nález, i když ne tak špatný, aby model dával odezvu větší než 0.5. Pak tento práh nebude 0.5, ale např. 0.4. Můžeš být zastánce přístupu "nejhorší je smrt z vystrašení" a rozhodneš se dovyšetřit jen pacienty s opravdu špatným nálezem. Pak nastavíš práh např. na 0.7. Jaký přístup je potřeba záleží na konkrétní situaci.
ROC křivka zobrazuje vztah mezi pravděpodobností detekce (true positive rate, senzitivita, recall) TPR a pravděpodobností falešného poplachu (false positive rate) FPR.
$$ TPR = \frac{TP}{P} = \frac{TP}{TP + FN}$$
$$ FPR = \frac{FP}{N} = \frac{FP}{FP + TN}$$
P, N ... jsou počty všech pozitivních/negativních vzorků
ROC křivka zobrazuje na ose x pravděpodobnost falešného poplachu, na ose y pravděpodobnost detekce. Toto pro všechny klasifikační prahy. Čím vyšší klasifikační práh, tím nižší pravděpodobnost falešného poplachu i nižší senzitivita. Čím menší klasifikační práh, tím větší pravděpodobnost detekce (senzitivita) i větší nebezpečí falešného poplachu.
from sklearn.metrics import plot_roc_curve
plot_roc_curve(klasifikator, X_test, y_test)
plot_roc_curve(dummy, X_test, y_test);
Hodnota AUC (Area Under the Curve) udává obsah plochy pod ROC křivkou. Čím větší plocha, tím lepší klasifikátor.