Shlukování (Clustering)
Shlukování (shluková analýza, clusterová analýza) je typickým představitelem strojového učení bez učitele. Problém k řešení spočívá v tom, že se neznámá data pokoušíme různými algoritmy rozdělit do skupin (shluků, clusterů) tak, aby v jedné skupině byla ta individua, která jsou si nejvíce podobná.
„Největší podoba“ přitom nejčastěji znamená, že jsou body v prostoru (individua), blízko u sebe. Prostor je definován jako v mnoha předchozích příkladech vlastnostmi zkoumaných objektů a počet těchto vlastností nám udává počet dimenzí. „Blízko u sebe“ je také možné definovat různými způsoby, které mají velký vliv na výsledek výpočtů. Asi nejznámějšími způsoby výpočtu vzdálenosti dvou bodů v prostoru jsou Euklidovská a Manhattanská vzdálenost. Obě je možné vidět na následujícím obrázku (zdroj).
Euklidovská vzdálenost je vyznačená zelenou čárou a jedná se o nejkratší vzdálenost mezi dvěma body. Manhattanská vzdálenost je inspirovaná pravoúhlým systémem křižovatek na Manhattanu a v obrázku ji reprezentují zbývající tři čáry, které, i když se to nemusí na první pohled zdát, mají všechny stejnou délku.
Tento obecný úvod má za cíl připomenout, že algoritmy strojového učení jsou často velmi obecné a finální výsledek velmi závisí na jejich správné volbě, nastavení, použitých metrikách a interpretaci výsledků. Takže ve finále výsledky rozhodně nejsou zadarmo.
My se v dnešních příkladech omezíme jen na Euklidovskou vzdálenost a pro názornost a snadnou vizualizaci na dvě dimenze, ale na konci si ukážeme použití i s více dimenzemi. Pro začátek si ukážeme, jak nejznámější shlukovací algoritmy fungují a jak si poradí s jednoduchými daty a pak vyzkoušíme složitější příklad.
k-means, k-median
Jedním z nejznámějších a také nejrychlejších shlukovacích algoritmů je k-means. Jeho princip je velice prostý:
- Na začátku se mezi body v prostoru vloží tzv. centroidy, což jsou body reprezentující středy výsledných shluků.
- Každý bod v prostoru se přiřadí k tomu centroidu, který je mu nejblíže. Dojde k prvnímu rozdělení na shluky.
- Centroidy se posunou tak, aby byly uprostřed mezi body, které v tu chvíli patří do jejich shluku. Zde je rozdíl mezi k-means a k-median ve výpočtu nové pozice pro centroidy, kdy první jmenovaný využívá průměr hodnot bodů ze stejného shluku, zatímco druhý jmenovaný využívá medián.
Body 2 a 3 se pak opakují tak dlouho, dokud nedojde k rovnovážnému stavu a pohyb centroidů se nezastaví. Celý proces je možné sledovat na následujících obrázcích, kdy každý z nich obsahuje jistou fázi od začátku až po ustálený stav.
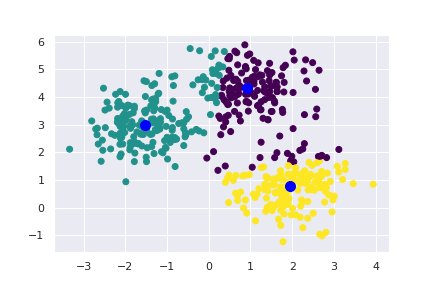
Po umístění centroidů a přiřazení bodů ke shlukům vidíme, že rozdělení není dokonalé.
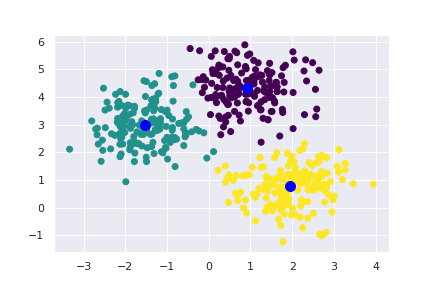
Po další iteraci je to daleko lepší, ale některé body ještě zbývá přesněji určit.
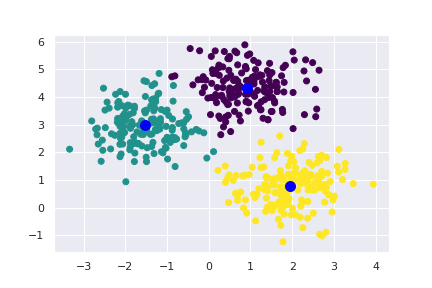
Velkou nevýhodou těchto jinak velmi dobře fungujících algoritmů je to, že jako vstupní parametr jim musíme zadat ono „k“, které určuje, kolik shluků hledáme a tedy kolik centroidů bude na začátku do prostoru umístěno. Je samozřejmě možné spustit k-means vícekrát s různým nastavením a sledovat vývoj výsledků.
Pojďme si to zkusit na náhodně generovaných datech.
from matplotlib import cm
from matplotlib import pyplot as plt
import seaborn as sns
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
%matplotlib inline
sns.set()
Nejprve si připravíme náhodně generovaná data pomocí funkce make_blobs.
X, y_true = make_blobs(n_samples=500, centers=4, cluster_std=0.50, random_state=0)
y_true obsahuje pro každý bod informaci, ke kterému shluku doopravdy patří. My se ovšem soustředíme na vizuální kontrolu výsledků.
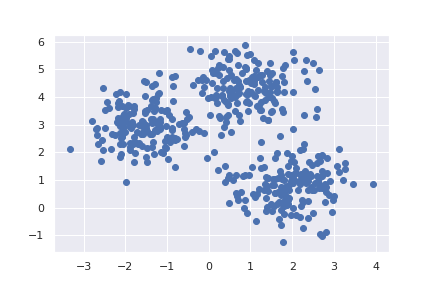
plt.scatter(X[:, 0], X[:, 1]);
V prostoru máme celkem 4 shluky a celkem 500 bodů. Nejprve můžeme vyzkoušet, co se stane, když k-means nastavíme rozdílný počet hledaných shluků.
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
vysledek = kmeans.predict(X)
centroidy = kmeans.cluster_centers_
plt.scatter(X[:, 0], X[:, 1], c=vysledek, cmap=cm.viridis);
plt.scatter(centroidy[:, 0], centroidy[:, 1], color="blue", s=20);
Na výsledné vizualizaci je vidět, že špatně zvolený počet hledaných shluků měl za následek spojení dvou oblastí do jedné. I když výsledek není nejlepší, je dobré si všimnout, že na dva ze čtyř shluků to nemá příliš zásadní vliv. Zkusme to ještě jednou a tentokrát správně.
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
vysledek = kmeans.predict(X)
centroidy = kmeans.cluster_centers_
plt.scatter(X[:, 0], X[:, 1], c=vysledek, cmap=cm.viridis);
plt.scatter(centroidy[:, 0], centroidy[:, 1], color="blue", s=20);
Teď už výsledek odpovídá našim představám a je z něj patrná i příslušnost ke shlukům u těch bodů, které jsou spíše na okraji svých shluků.
Hierarchické shlukování
Hierarchické shlukování obsahuje skupinu algoritmů, které při svém snažení postupují hierarchicky od jednotlivých bodů postupným připojováním k jednomu velkému shluku (aglomerativní metody) nebo od jednoho velkého shluku postupným dělením až k jednotlivým bodům (divisivní metody).
Podstatou je i zde měření vzdálenosti mezi jednotlivými body, mezi bodem a již existujícím shlukem nebo mezi dvěma shluky. Tyto vzdálenosti se mohou v závislosti na zvoleném typu podstatně lišit, jak demonstruje následující obrázek (zdroj).
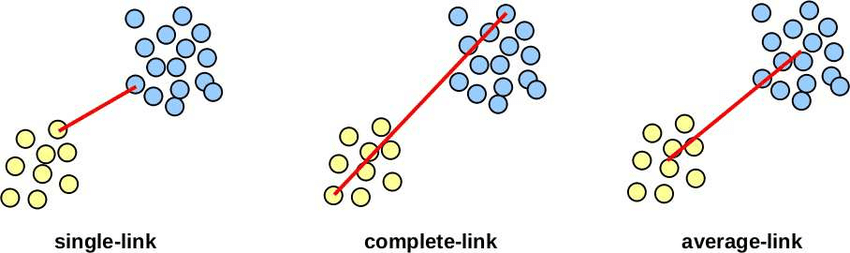
V praktickém pokusu se podíváme na stejná data jako před chvílí. K samotnému shlukování použijeme funkci linkage z modulu scipy.cluster.hierarchy. sklearn také obsahuje implementaci hierarchickéhu shlukování, konkrétně sklearn.cluster.AgglomerativeClustering, ale scipy nabízí i možnost snadného vykreslení tzv. dendrogramu. Dendrogram je grafickým znázorněním průběhu shlukování, který nám velmi názorně ukáže rozdíly ve vzdálenostech jednotlivých shluků.
from scipy.cluster.hierarchy import linkage, dendrogram
matice_vzdalenosti = linkage(X)
plt.figure()
dendrogram(matice_vzdalenosti)
plt.show()
Dendrogram výše znázorňuje proces shlukování. Úplně dole jsou nejdříve spojovány do menších shluků jednotlivé body, které postupně tvoří větší a větší shluky. Čím delší je svislá čára, tím větší vzdálenost musel algoritmus překonat, aby mohl dva shluky spojit v jeden. Na začátku jsou vzdálenosti krátké a tak spojení nic nebrání. Postupně je to ale čím dál tím horší a spojení dvou shluků napravo už není z hlediska vzdálenosti tak snadné. Následně se k těmto dvěma připojí téměř ihned shluk třetí a po nějaké chvíli dojde i ke spojení s posledním samostatným shlukem do jednoho velkého.
Dendrogram však sám o sobě není výsledkem shlukování. K tomu, abychom získali body rozdělené do shluků, musíme po prozkoumání dendrogramu říci, kolik shluků chceme případně jaká vzdálenost je pro nás již dostatečně velká, aby k dalšímu shlukování nedošlo. To vše se dá z dendrogramu vyčíst a následně aplikovat.
My známe počet shluků a tak je jejich zjištění z výsledku snadné.
from scipy.cluster.hierarchy import fcluster
vysledek = fcluster(matice_vzdalenosti, 4, criterion="maxclust")
plt.scatter(X[:, 0], X[:, 1], c=vysledek, cmap=cm.viridis);
Ovšem úplně stejně bychom si mohli říci, že vzdálenost 1.0 je pro nás hranice, nad kterou už shluky nechceme dále spojovat, a výsledek by byl stejný.
vysledek = fcluster(matice_vzdalenosti, 1.0, criterion="distance")
plt.scatter(X[:, 0], X[:, 1], c=vysledek, cmap=cm.viridis);
U vzdálenosti 1.5 už by došlo ke sloučení tří červených shluků a samostatně už by zůstal jen ten zelený.
vysledek = fcluster(matice_vzdalenosti, 1.5, criterion="distance")
plt.scatter(X[:, 0], X[:, 1], c=vysledek, cmap=cm.viridis);
DBSCAN
Třetím algoritmem do party je tzv. DBSCAN, tedy Density-Based Spatial Clustering of Applications with Noise, který, jak už jeho název napovídá, provádí shlukování na základě hustoty bodů v prostoru a je schopen detekovat šum — tedy body, které do žádného shluku nepatří.
DBSCAN si na začátku vezme jeden bod a prozkoumá jeho okolí. Pokud v tomto okolí najde dostatek sousedních bodů, označí je jako shluk a začne takto přeskakovat z jednoho bodu na další a přidávat je do stejného shluku. Pokud v okolí tohoto bodu není dostatek sousedů, je označen za šum. Jakmile je shluk kompletní a v okolí není žádný další bod k přezkoumání, vybere se další ještě nenavštívený bod a celý proces pokračuje stejným způsobem dále.
Z popisu je patrné, že na výsledek bude mít zásadní vliv prohledávané okolí bodu a počet sousedů, které je třeba najít, aby z nich mohl shluk vzniknout.
Zkusme tedy DBSCAN beze změny základních parametrů — prohledávané okolí 0,5; minimální počet sousedů 5 — pustit na naše testovací data.
from sklearn.cluster import DBSCAN
dbscan = DBSCAN()
vysledek = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=vysledek, cmap=cm.viridis);
Tento výsledek vypadá velmi dobře a oproti dříve představeným možnostem má tu výhodu, že nás upozorňuje i na šum — tedy na body, které jsou ve větší vzdálenosti od zbytku shluku a tedy do něj již nemusejí patřit.
DBSCAN má ještě jednu velkou výhodu — poradí si i se shluky, u kterých by si například k-means vylámal zuby.
from sklearn.datasets import make_circles
X, y_true = make_circles(n_samples=300, factor=0.2, random_state=0)
plt.scatter(X[:, 0], X[:, 1]);
dbscan = DBSCAN()
vysledek = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=vysledek, cmap=cm.viridis);
… a další
Shlukovacích algoritmů, principů a implementací existuje daleko více. My jsme si zde ukázali tři nejznámější zástupce tří různých kategorií. Hezký přehled je k dispozici na wikipedii a jejich implementace pak v sklearn.
Shluky kosatců
Zkusme si teď provést shlukovací analýzu známých kosatců z datasetu iris. Protože provádíme učení bez učitele, výsledky, které jsme používali u klasifikace, nás nebudou zajímat, a soustředíme se jen na vizuální kontrolu výsledku.
Kosatce, jak už víme, mají celkem 4 atributy (dva rozměry dvou druhů listů). U vizualizace si tedy nevystačíme s jedním grafem, ale využijeme pair plot nebo scatter matrix.
import pandas as pd # Seaborn neumí vizualizovat matice z numpy
from sklearn.datasets import load_iris
iris = load_iris()
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data
sns.pairplot(data);
Bez barevného rozlišení se zdá, že máme co dočinění jen se dvěma shluky. Uvidíme, jak se s tím poperou shlukovací algoritmy. Začneme s hierarchickým shlukováním, protože dendrogram nám může poskytnout užitečné informace.
matice_vzdalenosti = linkage(iris.data)
plt.figure()
dendrogram(matice_vzdalenosti)
plt.show()
A opravdu. Zdá se, že dva druhy kosatců k sobě mají velmi blízko a jsou vzdáleny od třetího druhu. Jaký výsledek dostaneme, když si od hierarchického modelu poručíme dva nebo tři clustery?
data["vysledek"] = fcluster(matice_vzdalenosti, 2, criterion="maxclust")
sns.pairplot(data, hue="vysledek", vars=['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']);
A pro očekávané tři shluky?
data["vysledek"] = fcluster(matice_vzdalenosti, 3, criterion="maxclust")
sns.pairplot(data, hue="vysledek", vars=['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']);
V tomto případě jsme se dočkali oddělení dvou bodů, které se v několika grafech zobrazují ve větší vzdálenosti od zbytku, do samostatného shluku.
Dočkáme se lepšího výsledku od k-means?
kmeans = KMeans(n_clusters=3, random_state=0)
kmeans.fit(iris.data)
data["vysledek"] = kmeans.predict(iris.data)
sns.pairplot(data, hue="vysledek", vars=['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']);
Zde je výsledek velmi zdařilý. To si říká o porovnání s originálními shluky, které máme k dispozici.
data["label"] = iris.target
sns.pairplot(data, hue="label", vars=['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']);
DBSCAN pro tuto úlohu není příliš vhodný, protože z grafů vidíme, že se nám dva shluky dost překrývají a tak by je DBSCAN buď spojil do jednoho, nebo by při opačném nastavení parametrů identifikoval menší části shluků jako samostatné shluky.
Závěr
Dnešní lekce měla ukázat základní možnosti strojového učení bez učitele na příkladech shlukování. Jak je vidět, výsledky opět velmi záleží na správném nastavení a volbě algoritmů a metrik, se kterými počítají. Možností a kombinací je u shlukování nepřeberné množství.